Unsteady Newtonian Flow
During the re-entry and hypersonic cruise the unsteady motion of the hypersonic vehicle is unavoidable. For this reason we have to determine the unsteady hypersonic aerodynamic coefficients in terms of time dependent pressure variation. Now, let us obtain the pressure coefficient expression of a body whose equation is given by B(x, y,z, t) = 0, has an instantaneous velocity of qB and is immersed in a free stream U as shown in Fig. 7.5.
If we denote the unit normal vector into the body with n then the normal velocity of the fluid particle that striking the surface of the body reads (Ui — qB).n. Afterwards, we can write the mass of the fluid particle which strikes onto the unit surface area in unit time becomes p (Ui — qB).n. According to the Newtonian impact theory, the momentum acting onto the surface of the body then becomes
The surface pressure coefficient at high Mach number is expressed from Eq. 7.15 as
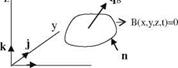 Fig. 7.5 Body B(x, y,z, t) = 0 z n„
Fig. 7.5 Body B(x, y,z, t) = 0 z n„
moving by velocity qB in a
U
Let us now write the unit normal vector n = li + mj + nk in terms of the direction cosines l, m, n of the surface equation B(x, y,z, t) = 0 as follows
Here,
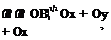 IgradB|
IgradB|
Unit normal n reads as
Let us express the instantaneous velocity qB in terms of its rectangular components qB = qxi + qyj + qzk. The normal component of the instantaneous velocity then reads as
If we assume that the body is rigid, then the shape of the body does not change but its position does in time. Therefore, dB/dt = 0 can be written as
![]() OB OB OB OB
OB OB OB OB
dB/dt = O + qx Ox + qy U + qz OZ =0
If we substitute Eqs. 7.17 and 7.18 into Eq. 7.16, the pressure coefficient then becomes
Writing the surface equation in terms of z, the equation becomes B = z — z1 (x, y,t) = 0.
O B Oz1 O B Oz1 O B Oz1
Ox Ox ’ Oy Oy ’ Ot Ot.
The surface pressure coefficient then reads
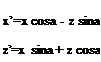 |
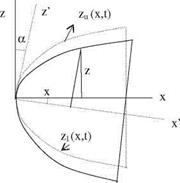 |
Example 7.1 The surface equation of a body is given by z = a(x/l)1/2, 0 < x < l. If this body pitches by a = a sin ю t about its nose in small amplitudes, find the surface pressure variation with time.
Solution: Let x, z be the fixed and the x’, z! be the rotating coordinate system. If we write the surface equation in terms of the fixed coordinates x, z then we have
![]() ‘ ‘ л 1 =2 x cos a — z sin a
‘ ‘ л 1 =2 x cos a — z sin a
zu = a(x ll) = a l———
Now, we can write B(x, z,t) = z’ — zu’ = 0 to give
(x cos a — z sin a112
B(x, z, t = x sin a + z cos a — a = 0.
Since the pitching oscillations are small, sin a = a and cos a = 1 yields
(x — za 1|2
B(x, z, t)=xa + z — a –
Now, we can use the last expression for B to be used in Eq. 7.20 to obtain the unsteady surface pressure coefficient. Here, we have to make a note that even a is small the Newton theory is non linear because of the last term in surface equation.
The Newton and the modified Newton theories are widely used for blunt bodies in engineering applications. For slender bodies, however, the Piston Analogy gives good results for the surface pressure expression in a hypersonic flow.











