Modal Characteristics of Bladed-Disks

The aim of this section is to elucidate in a qualitative manner how the previ­ous results inflience the stability of realistic bladed-disk configurations and in particular to discuss the relative merit of using cantilever, interlock or welded – pair configurations. Although there exists a big leap in moving from pure 2D to fully 3D mode shapes the simplicity of the approach makes the exercise still attractive.

The bladed-disk assembly considered in this study is representative of the first stages of modern LPTs. A global view of the whole assembly may be seen in figure 6. The vibration characteristics of the cantilever, interlock and welded-pair configurations has been obtained with the same grid. The bound­ary condition in the contact nodes between sliding parts, namely, between the disk and the blade in the attachment, and between the shroud contacts in the interlock configuration enforces that the displacements of these in both sides are identical. This simplifying hypothesis is made to avoid the generation of non-linear models where the concepts of natural frequency and mode-shape need to be re-interpreted.

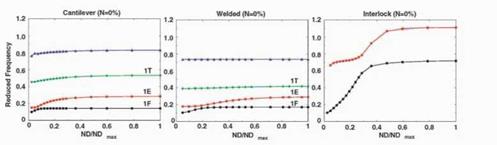
Since only the first two families are usually relevant for flitter studies we have restricted ourselves to the lowest range of the frequency – nodal-diameter diagram. Two analysis were carried out, firstly at rest and ambient tempera­ture and secondly at the operating sped with the associated temperatures. Only slight differences were seen in this particular case because the increase in stiff­ening due to the centrifugal force was compensated by the decrease in the Young’s module due to the increase in the inlet temperature of the turbine at the operating conditions. Since both results were very similar and to avoid further complications, the results presented correspond to the ones obtained at rest. The figure 7 shows the frequency characteristics of the first families for the cantilever (top), welded-pair (middle) and interlock (bottom) configu­rations. Several conclusions may be drawn upon inspection of this figure and the mode-shapes, not shown here for the sake of brevity,

1 The disk is very stiff compared to the blades. This may be seen in the mode-shapes, that show very small displacements of the disk, and in the frequency nodal diameter diagram that displays a high number of modes with nearly the same frequency within the same family.

2 The welded-pair configuration has slightly higher frequencies than the cantilever one with the exception of the third family that corresponds to the first torsion (1F) mode whose frequency drops.

3 The interlock provides and effective means to raise the frequencies of the assembly. The lower nodal diameters of the first family correspond to shroud dominated modes.

The baseline (cantilever) configuration is likely to be unstable since the re­duced frequency of the first fhp mode is too low, the first torsion mode is probably unstable a well. The welded-pair configuration is better from a flitter point of view than the cantilever one, the torsion mode will be stable in spite of having a lower reduced frequency, however, although the frequency of the 1st fhp mode is slightly higher than before, according with with the 2D inviscid results the mode is still unstable although the damping coefficient for the most unstable inter-blade phase angle has been reduced to one third of the original baseline configuration. This means that to predict absolute flutter boundaries three-dimensional and mistuning effects need to be retained.

The interlock configuration raises significantly the natural frequencies of the bladed-disk and hence is an effective mechanism as well to prevent flitter. A very similar interlock configuration was analyzed by Sayma et al. (1998), they found that the 6-12 nodal diameters, which corresponds in figure 7 (bot­tom) to 20% of the maximum nodal diameter, were unstable confirming pre­vious engine testing. A plausible explanation may be found by noting that the modes corresponding to the low diameter nodes of the interlock configuration are edgewise modes, which are stable, while the modes corresponding to the high diameter nodes are torsion modes, whose stability depends on the reduced frequency but that figure 3 (right) shows that is stable. The instability is con­centrated in the region where the edgewise modes become torsion modes and the reduced frequency is not high enough to ensure their stability.