True unsteady flow

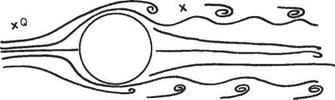
An example of true unsteady flow is the wake behind a bluff body, e. g. a circular cylinder (Fig. 2.2). The air is flowing from left to right, and the system of eddies or vortices behind the cylinder is moving in the same direction at a somewhat lower speed. This region of slower moving fluid is the ‘wake’. Consider a point P, fixed relative to the cylinder, in the wake. Sometimes the point will be immersed in an eddy and sometimes not. Thus the flow parameters will be changing rapidly at P, and the flow there is unsteady. Moreover, it is impossible to find a set of axes relative to which the flow is steady. At a point Q well outside the wake the fluctuations are so small that they may be ignored and the flow at Q may, with little error, be regarded as steady. Thus, even though the flow in some region may be unsteady, there may be some other region where the unsteadiness is negligibly small, so that the flow there may be regarded as steady with sufficient accuracy for all practical purposes.

Three concepts that are useful in describing fluid flows are:

(i) A streamline – defined as ‘an imaginary line drawn in the fluid such that there is no flow across it at any point’, or alternatively as ‘a line that is always in the same

Fig. 2.2 True unsteady flow

direction as the local velocity vector’ solid boundary it follows that:

Since this is identical to the condition at a

(a) any streamline may be replaced by a solid boundary without modifying the flow. (This only strictly true if viscous effects are ignored.)

(b) any solid boundary is itself a streamline of the flow around it.

(ii) A filament (or streak) line – the line taken up by successive particles of fluid passing through some given point. A fine filament of smoke injected into the flow through a nozzle traces out a filament line. The lines shown in Fig. 2.2 are examples of this.

(iii) A path line or particle path – the path traced out by any one particle of the fluid in motion.

In unsteady flow, these three are in general different, while in steady flow all three are identical. Also in steady flow it is convenient to define a stream tube as an imaginary bundle of adjacent streamlines.