Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
One-dimensional flow: the basic equations of conservation
A prime simplification of the algebra involved without any loss of physical significance may be made by examining the changes in the flow properties along a stream tube that is essentially straight or for which the cross-section changes slowly (i. e. so-called quasi-one-dimensional flow).
|
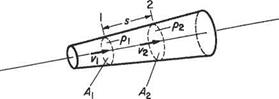
Fig. 2.3 The stream tube for conservation of mass The conservation of mass This law satisfies the belief that in normally perceived engineering situations matter cannot be created or destroyed. For steady flow in the stream tube shown in Fig. 2.3 let the flow properties at the stations 1 and 2 be a distance s apart, as shown. If the values for the flow velocity v and the density p at section 1 are the same across the tube, which is a reasonable assumption if the tube is thin, then the quantity flowing into the volume comprising the element of stream tube is: velocity x area = vi^i |
The mass flowing in through section 1 is
pvA (2.1)
Similarly the mass outflow at section 2, on making the same assumptions, is
P2V2A2 (2.2)
These two quantities (2.1) and (2.2) must be the same if the tube does not leak or gain fluid and if matter is to be conserved. Thus
PvA = p2v2A2 (2.3)
or in a general form:
pvA = constant (2.4)
