The measurement of air speed
1.3.1 The Pitot-static tube
Consider an instrument of the form sketched in Fig. 2.7, called a Pitot-static tube. It consists of two concentric tubes A and B. The mouth of A is open and faces directly into the airstream, while the end of В is closed on to A, causing В to be sealed off. Some very fine holes are drilled in the wall of B, as at C, allowing В to communicate with the surrounding air. The right-hand ends of A and В are connected to opposite sides of a manometer. The instrument is placed into a stream of air, with the
|
mouth of A pointing directly upstream, the stream being of speed v and of static pressure p. The air flowing past the holes at C will be moving at a speed very little different from v and its pressure will, therefore, be equal to p, and this pressure will be communicated to the interior of tube В through the holes C. The pressure in В is, therefore, the static pressure of the stream.
Air entering the mouth of A will, on the other hand, be brought to rest (in the ultimate analysis by the fluid in the manometer). Its pressure will therefore be equal to the total head of the stream. As a result a pressure difference exists between the air in A and that in B, and this may be measured on the manometer. Denote the pressure in A by pa. that in В by рв, and the difference between them by Дp. Then
&P = Pa— Pb (2.17)
But, by Bernoulli’s equation (for incompressible flow)
/>A+^p(0)2 =PB + ^pv1
and therefore
Ра~Ръ=^Р^ (2.18)
or
л 1 2
&P = 2PV
whence
v = y/lKpfp (2.19)
The value of p, which is constant in incompressible flow, may be calculated from the ambient pressure and the temperature. This, together with the measured value of Др, permits calculation of the speed v.*
The quantity ^pv2 is the dynamic pressure of the flow. Since рд = total pressure = po (i. e. the pressure of the air at rest, also referred to as the stagnation pressure), and рв = static pressure = p, then
Po~P = ^pv1 (2.20)
which may be expressed in words as
stagnation pressure — static pressure = dynamic pressure
It should be noted that this equation applies at all speeds, but the dynamic pressure is equal to jpv2 only in incompressible flow. Note also that
^pv2 = [ML-3L2T“2] = [ML-1T-2]
= units of pressure
as is of course essential.
* Note that, notwithstanding the formal restriction of Bernoulli’s equation to inviscid flows, the Pitot – static tube is commonly used to determine the local velocity in wakes and boundary layers with no apparent loss of accuracy.
|
P-Poo = ^(v2 – q*) |
|
|
|
|
|
|
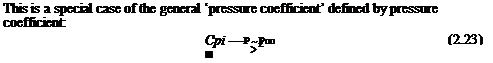 |
|
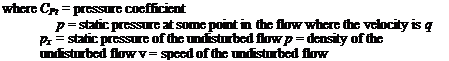 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|












