Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
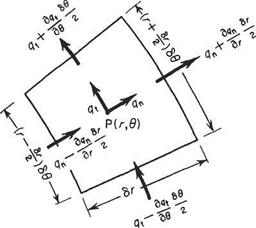
The equation of continuity in polar coordinates
 |
A corresponding equation can be found in the polar coordinates r and 6 where the velocity components are qn and qt radially and tangentially. By carrying out a similar development for the accumulation of fluid in a segmental elemental box of space, the equation of continuity corresponding to Eqn (2.44) above can be found as follows. Taking the element to be at P(r, 6) where the mass flow is pq per unit length (Fig. 2.13), the accumulation per second radially is:
|
|
|
|
 |
|
|
|
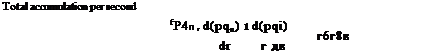and this by the previous argument equals the rate of change of mass within the region of space
|
д(ргбгбв) dt |
(2.51) |
|
Equating (2.50) and (2.51) gives: |
|
|
РЧ n dp d(pqn) 1 d(pq{) r dt dr r d0 |
(2.52) |
|
Hence for steady flow |
|
|
d{prqn) d{pql) dr de |
(2.53) |
|
and the incompressible equation in this form becomes: |
|
|
4n dqn 1 dql r dr r d0 |
(2.54) |
