Exact solutions of the Navier-Stokes equations

Few physically realizable exact solutions of the Navier-Stokes equations exist. Even fewer are of much interest in Engineering. Here we will present the two simplest solutions, namely Couette flow (simple shear flow) and plane Poiseuille flow (channel flow). These are useful for engineering applications, although not for the aerody­namics of wings and bodies. The third exact solution represents the flow in the vicinity of a stagnation point. This is important for calculating the flow around wings and bodies. It also illustrates a common and, at first sight, puzzling feature. Namely, that if the dimensionless Navier-Stokes equations can be reduced to an ordinary differential equation, this is regarded as tantamount to an exact solution. This is because the essentials of the flow field can be represented in terms of one or two curves plotted on a single graph. Also numerical solutions to ordinary differ­ential equations can be obtained to any desired accuracy.

1.9.1 Couette flow – simple shear flow

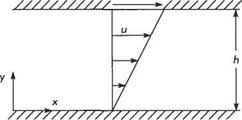
This is the simplest exact solution. It corresponds to the flow field created between two infinite, plane, parallel surfaces; the upper one moving tangentially at speed UT, the lower one being stationary (see Fig. 2.30). Since the flow is steady and two­dimensional, derivatives with respect to c and l are zero, and ir = 0. The streamlines

Fig. 2.30 are parallel to the x axis, so v = 0. Therefore Eqn (2.93) implies du/dx = 0, i. e. и is a function only of y. There is no external pressure field, so Eqn (2.92a) reduces to

r2

= 0 implying и = Cy + C2 (2.106)

where Ci and C2 are constants of integration, и = 0 and Uj when у = 0 and h respectively, so Eqn (2.106) becomes

и=иТт = – У (2.107)

h Ц

where r is the constant viscous shear stress.

This solution approximates well the flow between two concentric cylinders with the inner one rotating at fixed speed, provided the clearance is small compared with the cylinder’s radius, R. This is the basis of a viscometer – an instrument for measuring viscosity, since the torque required to rotate the cylinder at constant speed uj is proportional to r which is given by nuR/h. Thus if the torque and rotational speed are measured the viscosity can be determined.