Velocity components in terms of ф
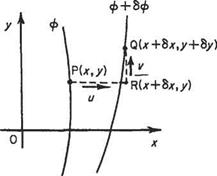
(a) In Cartesian coordinates Let a point P(x, y) be on an equipotential ф and a neighbouring point Q(x + 6x, y + 6y) be on the equipotential ф + 6ф (Fig. 3.4). Then by definition the increase in velocity potential from P to Q is the line integral of the tangential velocity component along any path between P and Q. Taking PRQ as the most convenient path where the local velocity components are и and v:
|
|
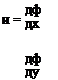 |
|
|
|
![]()
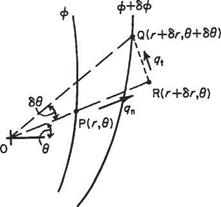
(b) In polar coordinates Let a point P(r, ff) be on an equipotential ф and a neighbouring point Q(r + Sr, в + 66) be on an equipotential ф + 6ф (Fig. 3.5). By definition the increase дф is the line integral of the tangential component of velocity along any path. For convenience choose PRQ where point R is (r + 6r, в). Then integrating along PR and RQ where the velocities are qn and qt respectively, and are both in the direction of integration:
бф = qnSr + qt(r + 6r)66
= qn6r + qtr66 to the first order of small quantities.
But, since ф is a function of two independent variables;
сі дф, дф
6ф=Tr6r * дё60
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) The velocity potential ф describes an irrotational flow in two dimensions where the velocity at any point is given by
дф дф
“ = а~х У = Щ (,v)
Substituting (iii) in (i) gives the identity
d2ip d2ip
dxdy ~ dxdy ~
which demonstrates the validity of (iii), while substituting (iv) in (ii) gives the identity
д2ф д2ф
dxdy dxdy
demonstrating the validity of (iv), i. e. a flow described by a unique velocity potential must be irrotational.
Alternatively substituting (iii) in (ii) and (iv) in (i) the criteria for irrotational continuous flow are that
![]() д2ф д2ф _ д2Ф д2,ф д7- + д?= = ~дх2+Ъу2
д2ф д2ф _ д2Ф д2,ф д7- + д?= = ~дх2+Ъу2
also written as Х72ф = Х72ф — 0, where the operator nabla squared
92 d2 dx2 + dy2
Eqn (3.4) is Laplace’s equation.











