Uniform flow
Flow of constant velocity parallel to Ox axis from left to right
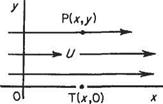
Consider flow streaming past the coordinate axes Ox, Oy at velocity U parallel to Ox (Fig. 3.9). By definition the stream function np at a point P(x, y) in the flow is given by the amount of fluid crossing any line between О and P. For convenience the contour
Fig. 3.9
OTP is taken where T is on the Ox axis x along from O, i. e. point T is given by (x, 0). Then
ip = flow across line OTP = flow across line ОТ plus flow across line TP = 0 + U x length TP
= 0 + Uy
Therefore
ip=Uy (3.12)
The streamlines (lines of constant ip) are given by drawing the curves
ip = constant = Uy
Now the velocity is constant, therefore
ip
у = — = constant on streamlines
The lines ip = constant are all straight lines parallel to Ox.
By definition the velocity potential at a point P(x, y) in the flow is given by the line integral of the tangential velocity component along any curve from О to P. For convenience take OTP where T has ordinates (x, 0). Then
ф = flow along contour OTP = flow along ОТ + flow along TP = Ux + 0
Therefore
![]()
 |
ф — Ux
The lines of constant ф, the equipotentials, are given by Ux = constant, and since the velocity is constant the equipotentials must be lines of constant x, or lines parallel to О у that are everywhere normal to the streamlines.











