Flow of constant velocity parallel to Oy axis

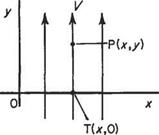
Consider flow streaming past the Ox, Oy axes at velocity Vparallel to Oy (Fig. 3.10). Again by definition the stream function ip at a point P(x, y) in the flow is given by the

Fig. 3.10 amount of fluid crossing any curve between О and P. For convenience take OTP where T is given by (jc, 0). Then

ф = flow across ОТ + flow across TP = —Vx + 0

Note here that when going from О towards T the flow appears from the right and disappears to the left and therefore is of negative sign, i. e.

ip = – Vx (3.14)

The streamlines being lines of constant ф are given by jc = —ф/V and are parallel to Оу axis.

Again consider flow streaming past the Ojc, Оу axes with velocity V parallel to the Оу axis (Fig. 3.10). Again, taking the most convenient boundary as OTP where T is given by (jc, 0)

ф = flow along ОТ + flow along TP = 0 +Vy

Therefore

ф=Уу (3.15)

The lines of constant velocity potential, ф (equipotentials), are given by Vy = constant, which means, since V is constant, lines of constant y, are lines parallel to Ojc axis.