Flow of constant velocity in any direction
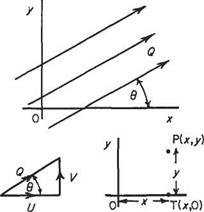
Consider the flow streaming past the jc, у axes at some velocity Q making angle 9 with the Ojc axis (Fig. 3.11). The velocity Q can be resolved into two components U and V parallel to the Ojc and Оу axes respectively where Q2 = U2 + V2 and tan# = V/U.
Again the stream function ф at a point P in the flow is a measure of the amount of fluid flowing past any line joining OP. Let the most convenient contour be OTP, T being given by (jc, 0). Therefore
Fig. 3.11
ф = flow across ОТ (going right to left, therefore negative in sign)
+ flow across TP
=— component of Q parallel to Oy times x + component of Q parallel to Ox times у rp = —Vx+Uy (3-16)
Lines of constant ф or streamlines are the curves
– Vx + Uy = constant
assigning a different value of ф for every streamline. Then in the equation V and U are constant velocities and the equation is that of a series of straight lines depending on the value of constant ф.
Here the velocity potential at P is a measure of the flow along any curve joining P to O. Taking OTP as the line of integration [T(x, O)]:
ф = flow along ОТ + flow along TP
![]()
 |
= Vx + Vy ф = Ux+ Vy
Example 3.1 Interpret the flow given by the stream function (units: m2 s ‘)
ф = 6x + 12у
The constant velocity in the horizontal direction = ^ = +12ms-1
dy
The constant velocity in the vertical direction =-^ = -6ms_I
ox
Therefore the flow equation represents uniform flow inclined to the Ox axis by angle $ where tan# = —6/12, i. e. inclined downward.
The speed of flow is given by
Q = ч/б2 + 122 = 7l80ms-1











