A source in a uniform horizontal stream
Let a source of strength m be situated at the origin with a uniform stream of — U moving from right to left (Fig. 3.13).
Then
![]() (3.18)
(3.18)
which is a combination of two previous equations. Eqn (3.18) can be rewritten
![]() ф = tan 1 – — Uy
ф = tan 1 – — Uy
2тг x
to make the variables the same in each term. Combining the velocity potentials:
or
![]() (3.20)
(3.20)
or in polar coordinates
![]() m r
m r
ф = —In—- UrcosO
2тг r0
These equations give, for constant values of ф, the equipotential lines everywhere normal to the streamlines.
Streamline patterns can be found by substituting constant values for ф and plotting Eqn (3.18) or (3.19) or alternatively by adding algebraically the stream functions due to the two cases involved. The second method is easier here.
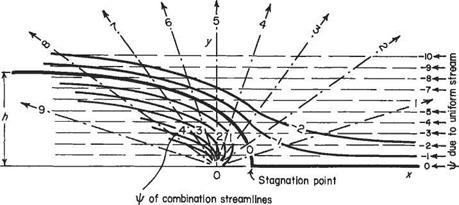
Method (see Fig. 3.14)
(1) Plot the streamlines due to a source at the origin taking the strength of the source equal to 20m2s_I (say). The streamlines are тг/10 apart. It is necessary to take positive values of у only since the pattern is symmetrical about the Ox axis.
(2) Superimpose on the plot horizontal lines to a scale so that ip = — (Jy = — I, —2, —3, etc., are lines about 1 unit apart on the paper. Where the lines intersect, add the values of ip at the Unes of intersection. Connect up all points of constant – ip (streamlines) by smooth lines.
The resulting flow pattern shows that the streamlines can be separated into two distinct groups: (a) the fluid from the source moves from the source to infinity without mingling with the uniform stream, being constrained within the streamline ip = 0; (b) the uniform stream is split along the Ox axis, the two resulting streams being deflected in their path towards infinity by – ip = 0.
It is possible to replace any streamline by a solid boundary without interfering with the flow in any way. If – ip = 0 is replaced by a solid boundary the effects of the source are truly cut off from the horizontal flow and it can be seen that here is a mathematical expression that represents the flow round a curved fairing (say) in a uniform flow. The same expression can be used for an approximation to the behaviour of a wind sweeping in off a plain or the sea and up over a cliff. The upward components of velocity of such an airflow are used in soaring.
The vertical velocity component at any point in the flow is given by —dip/dx. Now
V^tan-‘Q-t/y (Eqn(3.19))
дф _ m 9tan-I(y/x) d(y/x) дх 2-її d(y/x) dx
2tt 1 + (y/xf x2
![]()
|
|
_дФ_п_т * T, U ду ° 2tt x2+y2 U = ^ = n= m У dx 2-k x2 + y2 |
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|
||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|
||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|
|
|
|
|
2тгх2 + у2
from which the local velocity can be obtained from q = /u2 + v2 and the direction given by tan-1 (v/u) in any particular case.