Source-sink pair

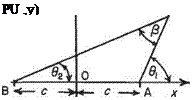
This is a combination of a source and sink of equal (but opposite) strengths situated a distance 2c apart. Let ±m be the strengths of a source and sink situated at points A (c, 0) and В (—c, 0), that is at a distance of c m on either side of the origin (Fig. 3.15). The stream function at a point P(jc, у), (г, 0) due to the combination is

(3.26)

Transposing the equation to Cartesian coordinates:

Therefore

(3.27)

and substituting in Eqn (3.26):

(3.28)

To find the shape of the streamlines associated with this combination it is neces­sary to investigate Eqn (3.28). Rearranging:

or

x2 +У2 — 2ccot^^y — c2 = 0 m

which is the equation of a circle of radius csjcot2 (2тгф/т) + 1, and centre ccot(2Tnp/m).

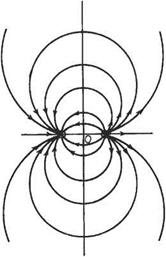
Therefore streamlines for this combination consist of a series of circles with centres on the Оу axis and intersecting in the source and sink, the flow being from the source to the sink (Fig. 3.16).

Consider the velocity potential at any point P(r, 9){x, y).*

m r m r2 m, r i

: — In — – — In — = — In —

27Г r0 2tt ro 2іг Г2

rf = (x — c)2+y2 = x2+y2 + c2 — 2 xc = (x + c)2 + y2 = x2 + y2 + c2 + 2 xc

Fig. 3.16 Streamlines due to a source and sink pair

* Note that here r0 is the radius of the equipotential ф = 0 for the isolated source and the isolated sink, but not for the combination.

Therefore, the equipotentials due to a source and sink ombination are sets of eccentric non-intersecting circles with their centres on the Ox axis (Fig. 3.17). This pattern is exactly the same as the streamline pattern due to point vortices of opposite sign separated by a distance 2c.