Prandtl’s mixing-length theory of turbulence
Equation (7.111) is not a good approximation in the region of the turbulent boundary layer or pipe flow near the wall. The eddy viscosity varies with distance from the wall in this region. A commonly used approach in this near-wall region is based on
 |
|
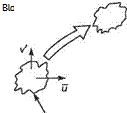
Fig. 7.36
Prandtl’s mixing-length theory.[41] This approach to modelling turbulence is loosely based on the kinematic theory of gases. A brief account is given below and illustrated in Fig. 7.36.
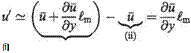 |
Imagine a blob of fluid is transported upward by a fluctuating turbulent velocity v’ through an average distance im – the mixing length – (analogous to the mean free path in molecular dynamics). In the new position, assuming the streamwise velocity of the blob remains unchanged at the value in its original position, the fluctuation in velocity can be thought to be generated by the difference in the blob’s velocity and that of its new surroundings. Thus
Term (i) is the mean flow speed in the new environment. In writing the term in this form it is assumed that im <C 8, so that, in effect, it is the first two terms in a Taylor’s series expansion.
Term (ii) is the mean velocity of blob.
If it is also assumed that V ~ (du/dy)£m, then
 (7.112)
(7.112)
Term (iii) is written with an absolute value sign so that the Reynolds stress changes sign with дй/ду, just as the viscous shear stress would.











