Activity factor
The activity factor is a measure of the power-absorbing capacity of the airscrew, which, for optimum performance, must be accurately matched to the power produced by the engine.
![]() Consider an airscrew of diameter D rotating at n with zero forward speed, and consider in particular an element of the blade at a radius of r, the chord of the element being c. The airscrew will, in general, produce a thrust and therefore there will be a finite speed of flow through the disc. Let this inflow be ignored, however. Then the motion and forces on the element are as shown in Fig. 9.3. 1
Consider an airscrew of diameter D rotating at n with zero forward speed, and consider in particular an element of the blade at a radius of r, the chord of the element being c. The airscrew will, in general, produce a thrust and therefore there will be a finite speed of flow through the disc. Let this inflow be ignored, however. Then the motion and forces on the element are as shown in Fig. 9.3. 1
![]()
|
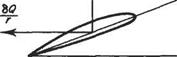
Fig. 9.3
and therefore the torque associated with the element is
SQ = 2ir1pCj}nl(cri)Sr
It is further assumed that Co is constant for all blade sections. This will not normally be true, since much of the blade will be stalled. However, within the accuracy required by the concept of activity factor, this assumption is acceptable. Then the total torque required to drive an airscrew with В blades is
Thus the power absorbed by the airscrew under static conditions is approximately
In a practical airscrew the blade roots are usually shielded by a spinner, and the lower limit of the integral is, by convention, changed from zero (the root) to 0.1 D. Thus
Defining the activity factor (AF) as
leads to
Further work on the topic of airscrew coefficients is most conveniently done by means of examples.
Example 9.3 An airscrew of 3.4 m diameter has the following characteristics:
Calculate the forward speed at which it will absorb 750 kW at 1250 rpm at 3660 m (a = 0.693) and the thrust under these conditions. Compare the efficiency of the airscrew with that of the ideal actuator disc of the same area, giving the same thrust under the same conditions.
Power = 2m Q
Therefore
„ 750000×60 „„Л1кТ
torque g= 27rxl250 = 5730 Nm
![]() = 20.83 rps n1 = 435 (rps)2
= 20.83 rps n1 = 435 (rps)2
Therefore
Plotting the given values of kg and 77 against J shows that, for kg = 0.0368, J = 1.39 and 77 = 0.848. Now J = V/nD, and therefore
V = JnD = 1.39 x 20.83 x 3.4 = 98.4ms_I
Since the efficiency is 0.848 (or 84.8%), the thrust power is
750 x 0.848 = 635 kW
Therefore the thrust is
![]()
![]()
Power 635000 T = г = = 6460 N
whence
a = 0.0417
Thus the ideal efficiency is
Thus the efficiency of the practical airscrew is (0.848/0.958) of that of the ideal actuator disc. Therefore the relative efficiency of the practical airscrew is 0.885, or 88.5%.
![]()
Example 9.4 An aeroplane is powered by a single engine with speed-power characteristic:
The fixed-pitch airscrew of 3.05m diameter has the following characteristics:
|
J |
0.40 |
0.42 |
0.44 |
0.46 |
0.48 |
0.50 |
|
кт |
0.118 |
0.115 |
0.112 |
0.109 |
0.106 |
0.103 |
|
kQ |
0.0157 |
0.0154 |
0.0150 |
0.0145 |
0.0139 |
0.0132 |
and is directly coupled to the engine crankshaft. What will be the airscrew thrust and efficiency during the initial climb at sea level, when the aircraft speed is 45ms~’?
Preliminary calculations required are:
Q = kepn2D5 = 324.2 kQn2
after using the appropriate values for p and D.
J = V/nD = 14.75/n
The power required to drive the airscrew, Pr, is
Pr = 2 miQ
With these expressions, the following table may be calculated:
|
rpm |
1800 |
1900 |
2000 |
2100 |
|
Fa(kW) |
1072 |
1113 |
1156 |
1189 |
|
n (rps) |
30.00 |
31.67 |
33.33 |
35.00 |
|
/72(rps)2 |
900 |
1003 |
1115 |
1225 |
|
J |
0.492 |
0.465 |
0.442 |
0.421 |
|
kQ |
0.013 52 |
0.01436 |
0.01494 |
0.015 38 |
|
G(Nm) |
3950 |
4675 |
5405 |
6100 |
|
P r(kW) |
745 |
930 |
1132 |
1340 |
In this table, P3 is the brake power available from the engine, as given in the data, whereas the values of kQ for the calculated values of J are read from a graph.
A graph is now plotted of P3 and PT against rpm, the intersection of the two curves giving the equilibrium condition. This is found to be at a rotational speed of 2010 rpm, i. e. n = 33.5 rps. For this value of n, J = 0.440 giving kT = 0.112 and kQ = 0.0150. Then
T = 0.112 x 1.226 x (33.5)2 x (3.05)4 = 13 330N
and
As a check on the correctness and accuracy of this result, note that
thrust power = TV = 13 300 x 45 = 599 кW
At 2010 rpm the engine produces 1158kW (from engine data), and therefore the efficiency is 599 x 100/1158 = 51.6%, which is in satisfactory agreement with the earlier result.











