UNSTEADY AERODYNAMIC FORCES ON AN AIRFOIL IN AN INCOMPRESSIBLE FLUID

The simplified analysis of the preceding sections are based on the quasi-steady aerodynamic derivatives. We shall now show how the quasi-steady assumptions can be removed. In this and later sections, the results of the linearized aerodynamic theory, as presented in Chapters 12-15, will be used.

In order to show the existence of the critical flutter conditions, we shall first summarize the aerodynamic forces acting on a two-dimensional

airfoil in unsteady motion in an incompressible fluid. The equations of motion of the airfoil are derived in § 6.8. The forced oscillation of the airfoil due to a periodic excitation is then considered in § 6.9. Following this, in § 6.10, the flutter of a two-dimensional airfoil is discussed in general terms, without restricting to the incompressible fluid. The solu­tion of the flutter determinant and a summary of the methods of deter­mining the critical speeds are presented in the last two sections.

The unsteady aerodynamic force acting on a thin airfoil in unsteady

* In the definition of the critical reduced frequency of flutter, со is the frequency at the critical flutter speed, which, in general, differs somewhat from the fundamental frequency of the torsional oscillation of the wing. But, since the flexural rigidity plays only a minor part in the flexure-torsional flutter, the “apparent” reduced frequency as defined above has a physical significance.

motion in a two-dimensional incompressible fluid was obtained by Wagner, Kiissner, von Karman and Sears, and others. Let the chord of the airfoil be 2b, and the angle of attack (assumed infinitesimal) a. Con­sider the growth of circulation about the airfoil which starts impulsively from rest to a uniform velocity U. Let the impulsive motion take place at the origin when г = 9 (Fig. 6.5). The vertical velocity component of the fluid, the so-called downwash, is w = U sin a = 17a on the airfoil, since the flow must be tangent to the airfoil. Then, on the physical assumption that the velocity at the trailing edge must be finite, one derives the lift due to circulation on a strip of unit span as a function of time:

Lx = IrrbpUw Ф(т), Ф(т) = 0 if т < 0 (1)

where

т = Ut/b (2)

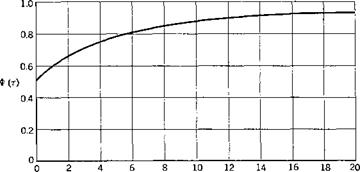
is a nondimensional quantity proportional to time. The function Ф(т), called Wagner’s function, is illustrated in Fig. 6.6. An approximate

r, distance traveled, in semichords Fig. 6.6. Wagner’s function for an incompressible fluid.

expression which agrees within 2 per cent of the exact value in the entire range 0 < t < oo is given by Garrick15-9’ 15-17:

ф(т) – і _ JL_ (T > 0) (3)

4 – f – t

Another approximate expression is given by R. T. Jones15-43:

Ф(т) = 1 – 0.165<?~°’0455t – 0.335е~аз00т (т > 0) (4)

whereas W. P. Jones gives15-80

Ф(т) = 1 – 0.165e-°-04lT – 0.335e-°-32r

The expression 4a gives slightly better approximation than Eq. 4 for

T < 2.2.

The exact form of Ф(т) is the following (see § 15.1)

ф(т) = l – Ґ “{(*„ – Kxf + ттЦі0 + dx (5)

Jo

where K0, Kx /„, Ix are modified Bessel functions of the second and first kind, respectively, with argument x implied. It is seen that half of the final lift is assumed at once and that the lift approaches asymptotically its steady-state value 2irbpUw when т -> со. The center of pressure of this lift (due to circulation) is at the 1/4-chord point behind the leading edge.

Let us now consider a more general type of motion. Let the airfoil have two degrees of freedom: a vertical translation h, called bending, positive downward, and a rotation a, called pitching, positive nose up, about an axis located at a distance ahb from the mid-chord point, ah being positive toward the trailing edge (Fig. 6.7).* The flow is assumed to be two-dimensional, h and a are infinitesimal, and the mean flow speed U is a constant. In this case part of the lift arises from circulation, and part from noncirculatory origin—the so-called “apparent mass” forces.

Wagner’s function gives the growth of circulation about the airfoil due to a sudden increase of downwash which is uniform over the airfoil. For a general motion having two degrees of freedom h and a, the down – wash over the airfoil is not uniform. Now, in the theory of oscillating airfoils, it can be shown that for bending and pitching oscillations the circulation about the airfoil is determined by the downwash velocity at the 3/4-chord point from the leading edge of the airfoil (§ 13.4). By a reciprocal relation between the harmonic oscillations and the response to unit-step functions (§ 15.1), and the principle of superposition, this result holds also for arbitrary bending and pitching motions. Hence, if we replace w in Eq. 1 by the increment of downwash at the 3/4-chord point, the circulatory lift can be obtained.

The downwash at the 3/4-chord point due to the h and a degrees of freedom consists of the following: (1) a uniform downwash corresponding to a pitching angle a, w — V sin a = t/a (a being infinitesimal), (2) a uniform downwash due to vertical translation h, which may also be written

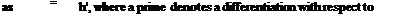
the nondimensional time t, and a dot denotes a differentiation with respect

* These notations are different from those of the preceding sections. In the airfoil theory (Chapters 12-15), the origin of reference axes is usually taken at the mid-chord point, and the semichord length b is taken as the characteristic length. In keeping with these standard notations, the symbols are redefined in Fig. 6.7.

to the physical time t, (3) a nonuniform downwash due to a, its value at

the 3/4-chord point being (V2 — ah)b — or (1/2 — ah)Ua!.

dt

Summing up, we find

w(r) = Ua(r) + jh'(r) + (i — ah)Ua(r) (6)

In the time interval (r0, r0 + dr0), the downwash w(r0) increases by an

amount сіт0. When dr0 is sufficiently small, this may be regarded dr0

as an impulsive increment and the corresponding circulatory lift per unit span is

, dw(r0)

■ t0) j— «To for T 3» t„ drn

By the principle of superposition which holds when w remains small, we have the circulatory lift per unit span for arbitrary time history of w:*

Cr dw

Lfj) = 2-rrbpU Ф(т — r0) — (r0) dr0 (7)

J— CO UTq

where the lower limit is taken as — oo, meaning before the very beginning of motion. If the motion starts at time r = 0, w — 0 for r < 0, Eq. 7 reduces to

where w0 is the limiting value of w(r) when r -> 0 from the positive side. f It is, of course, to be remembered that Ф(т — r0) = 0 if r < r0. Com­bining Eq. 7 with Eq. 6, we obtain:

*'(t0) + ~bh"(r0) «ftj a"(To)

An expression corresponding to Eq. la can be written down if the motion starts at time r = 0.

When the airfoil has a general motion, the lift and moment of the noncirculatory origin (the apparent mass forces) must be added. The resultant lift and moment include the following terms:

1. A lift force with center of pressure at the mid-chord, of amount equal to the apparent mass prrb2 times the vertical acceleration at the mid-chord point:

L2 = pnb2(h — ahba.) = pnU2(h" — ahboc") (9)

* Duhamet’s integral. See §8.1.

t The first term in Eq. 7a gives the effect of initial disturbance. It can be obtained formally from Eq. 7 by noticing the jump of w(t0) at r0 = 0.

2. A lift force with center of pressure at the 3/4-chord point, of the nature of a centrifugal force, of amount equal to the apparent mass рттЬ2 times Ш.. (This term is, however, circulatory.)

L3 = рттЬ2Ш. = рттЬ U2a (10)

3. A nose-down couple equal to the apparent moment of inertia* рттЬ2(Ь2/&) times the angular acceleration к:

pnb2U2 „

8

The total lift per unit span is then

L = + L% – p L3 (12)

The total moment per unit span about the elastic axis is

M = (i + ajbL, + ahbL2 – (i – ah)bL3 + Ma (13)

All these are valid for a two-dimensional flow of an incompressible fluid.