SOME MATHEMATICAL CONCEPTS

The Concept of Complex Impedance and Admittance. In § 1.8, it is shown that the steady-state solution of the equation

272

SEC. 8.1	SOME MATHEMATICAL CONCEPTS	273
d2x m~di2	dx + p – + Kz = (p> 0)	(1)
may be written	as	F Jut	(2)
where		Z(/a>) = m(ico)2 + f>(ioj) + К	(3)

Equations 1 and 2 may be compared to the relations between the electromotive force E{t) and the current I{t) flowing in an electric circuit:

L~ + Rl+r; (Idt = E dt C Jo (4)

/(0 = E(t)IZ

where Z is the impedance of the circuit which depends on the frequency со of the electromotive force, the inductance L, resistance R, and the capitance C of the circuit:

Z = icoL + R + (5)

icoC

By the anology between Eqs. 2 and 4, Z(iaj) is called the impedance of the system represented by Eqs. 1. – If Eq. 1 represents a mechanical system, Z(ico) may be called the mechanical impedance. Its inverse, l/Z(ico), is called the admittance.

The response of a linear system to an exciting force that varies har­monically is simply given by multiplying the exciting force by the admit­tance.

In engineering literature a different notation is often used by putting s = /со and writing Z(s) instead of Z(ico). Note that Z(s) can be obtained directly from the differential equation by a formal process of replacing

the operator d/dt by the symbol s, and J dt by 1 js.

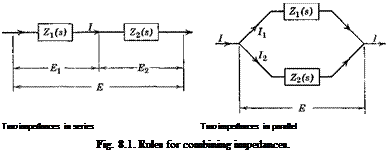
The rules for calculating the impedance of a circuit are the same as those for combining the electrical resistance. Thus (Fig. 8.1), if Z1 and Z2 are in series, the resultant impedance is

Z = Zi + Z2 (6)

On the other hand, if Zx and Z2 are in parallel, the resultant Z is given by the equation

1 = 1 + 1 z Zj z2

The Principle of Superposition. Since the differential equation 1 is linear, the principle of superposition holds. In particular, if the right – hand side of Eq. 1 is

Fft) + Fft) = F10eM + F20ei2ra( a particular solution will be

■’T і 2_ Z(ia>) Z(i2a>)

More generally, if the right-hand side is given by a Fourier series

(8)

then

As a further generalization, if F(t) is represented by a Fourier integral m = where V2t7 . 1 | А{ы)еш dm )— CO Г c° (10) А(ш) = V2tt. F{t)e-Wt dt ) — 00 then a particular solution is x(t) = 1 s/2n * (11)

These processes can be justified if the right-hand sides of Eqs. 9 and 11 converge (see Chapters IX and X of Karman and Biot154).

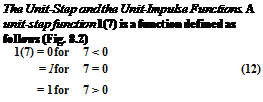m

1

t——— *-

Unit step function.

If the point of jump is moved to the point t = t, the unit-step function is written as 1(7 — r) for which

1(7 — r) = 0 for 7 < r

= | for 7 = t (13)

= 1 for 7 > r

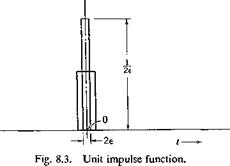A unit-impulse function (5(7) is a function that is zero for 7 < — e and t > є, є being any positive number, but tends to oo when 7 = 0, and

the integral of (5(7) taken over the interval — £ to є is equal to 1 (Fig. 8.3). Thus, if (5(7) denotes the unit-impulse function, then (5(7) = 0 for 7 Ф 0

lim Г (5(7) dt = 1 (14)

£—>■0 J — Є

Whereas the unit-step function is well defined, the unit-impulse function, mathematically speaking, is not. But, since its introduction by Dirac,
the unit-impulse function (often called the Dirac (5-function) has become a powerful tool for physicists.[21]

Let us quote without proof (for a proof, see, for example, K&rm&n and Biot,154 pp. 394-396) the following integral representations of the unit-step and unit-impulse functions

(15)

(16)

Indicia! Admittance. The response of a physical system to a unit-step function is called the indicial admittance. In some cases the indicial admittance can be found by elementary methods. In general, the method of Laplace transformation (Chapter 10) gives the solution readily.

Consider the equations

The general solution of the differential equation is

x = —- + Cx sin co0t + C2 cos co0t Щ

Using the initial conditions, we find Cx = 0, C2 = — l/co02. Hence, the indicial admittance is

A(t) = x = – i; (1 — cos «„01(0 (18)

COq

Example 2. Consider the same problem with the right-hand side replaced by a unit-impulse function.

Integrating the differential equation from — e to є, where є is a small number, we obtain

f£ d2x Ce

L^dt+^Lxdt = 1 (20)

The first integral in the above equation can be written as fe d ldx fe,(dx dx e (dx

J-. dt W dt Ы “ Jt Ы1-. (21)

since (dx/dt=_e — 0. The second integral in Eq. 20 tends to zero when є tends to zero, because, in the neighborhood of f = 0, |ж| is a finite number, say < K, and the integral is bounded by 2Ke, which vanishes in the limit є -> 0. Hence, in the limit, Eq. 20 becomes

The given system (Eqs. 19) is then equivalent to the following d*x

dt/t=e

the solution of which is

h(t) = — sin co0t 1(f) co0

Note that the results of Exs. 1 and 2 are related by the equation

dA

dt

A more general result, valid also when A(0) Ф 0, is (see Karman and Biot,1-54 p. 402)

dA

dt

where A(t) is the indicial admittance and h(t) the response to a unit – impulse function.

Duhamel’s Integral. When the governing equation is linear, the principle of superposition holds. Thus, the response to the sum of two

step functions is the sum of the indicial admittances. In other words, the response to a function

C 1(0 Ч – c2 io t)

is

cx A(t) + c2 A(t — r)

where A(t) is the indicial admittance to 1(0- Now any function f(t), having a continuous derivative, can be repre­sented in the integral form

Л’)-/т+[£(г)4г

= /(0) 1(0 +£ f(0 10 – r) dr (25)

Since an integration is the limit of a summation, and since for each

jf

element “ (т) 1(г — r) dr the response is dt

Jt (0 A{t — t) dr

we obtain by the principle of superposition that the response to the function f(t) is

x(t) =/(0) A(t) + [ I(r) A(t – r) dr (26)

Integrating by parts, we obtain an equivalent form:

rt dA

x(t) =/(0 Д0) +Jo/(r) — 0-t) dr (27)

The integrals in Eqs. 25, 26, and 27 are known as Duhamel integrals.

By Eq. 24, the Duhamel integral 27 can be written as

Дт) hit — r) dr (28)

where h(r) is the response to a unit-impulse function.

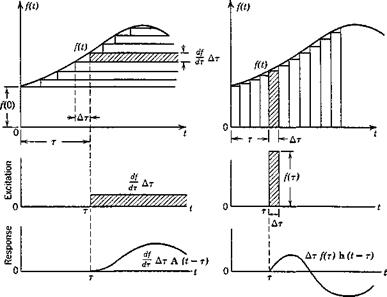
A graphical interpretation of these results is originated by von Kdrmdn and Biot1-64 and is given in Fig. 8.4 which seems to be self-explanatory.

Relation between the Admittance and the Indicial Admittance. Perhaps the harmonic function is the simplest periodic function, and the unit-step function is the simplest nonperiodic function. Nevertheless, any arbitrary function, under very mild mathematical restrictions on continuity and differentiability, can be resolved, either into simple-harmonic components

in the form of a Fourier integral, or into unit-step functions by means of a Duhamel integral. Knowing either the impedance or the indicial admittance, we can derive the response to an arbitrary forcing function by a single integration. Hence, the problem of dynamic responses resolves ultimately into finding either the indicial admittance or the impedance.

In particular, the indicial admittance can be determined from the admittance by an integration, and vice versa. In fact, since the Fourier representation of the unit-step function is Eq. 15, and since the impedance

Fig. 8.4. Duhamel integral. Illustrations by von Karmdn and Biot, Ref. 1.54. (Courtesy of McGraw-Hill Book Co.).

of a component eim4{(S + im) is (fi 4- im)Z(im), we can write the indicial admittance A(t) as

J Л CO gialt

A(,) – 2- s J-. <p+»№) (29)

If the physical system is undamped, so that Z(im) vanishes at some real number со, the integral in Eq. 29 becomes divergent. A convergent result can usually be obtained by introducing a “convergence factor,” /8 > 0, into the impedance Z(/co), and writing

1 fю еш

A(t) = — lim ——————– —————- dm

2tt p-+o J-ш (/? – f io))Z(f> 4- m)

This is a Fourier integral. If we put

(31)

where c is a positive number greater than the real part of all the roots of Z(s) = 0. But Eq. 31 is the Bromwich’s integral which represents the inversion of a Laplace transform (cf. Eq. 2 of § 10.1). By the transform pair of Laplace transformation, we obtain

(32)

In other words, l/sZ(s) is the Laplace transform of A(t), and A(t) is the inverse Laplace transform of 1 /sZ(s).