GENERAL EQUATIONS

Let a system of rectangular coordinates (x, y) be taken, with the x axis parallel to the flow at infinity, and with the origin at a fixed point which

395

is the mean position of the mid-chord point of the airfoil. The mean chord of the airfoil lies along the x axis. Let the scale be so chosen that the semichord length is equal to unity. Therefore the projection of the leading edge of the airfoil is at x = — 1, and that of the trailing edge is at x — + 1. Let the airfoil be described by the equation

у = Y(x, t) (- 1 < * < 1) (1)

(See Fig. 13.1.) It is assumed that Y and dY/dx are so small that the skeleton airfoil does not differ appreciably from a horizontal line. The disturbances caused by the motion of the airfoil are therefore small.

The velocity (и, v) of the fluid consists of a uniform mean velocity (U, 0) in the direction of the positive x axis, and a small perturbation (и’, v’):

и = U + г/ (И < U)

(2)

v — v’ (|г/| U)

The acceleration components a’x and a’y are linearized into

diY, ди’ Эи’ ди’ Эu’

; +(C/+C/_

Эv’ dv’ ,dv’ dv’ dtf

:_ + (С/+г/)__-_г;__=__+г7_

when small quantities of the second order are neglected. Since the fluid is assumed to be incompressible, p = const; the acceleration potential </>’ is proportional to the change of pressure p’

рф’=-Ґ

and is governed by the equation

As shown in § 12.5, there exists a pair of conjugate harmonic functions ф’ and tp’, so that

w = f + jY = f(x + jV) (6)

is an analytic function of a complex variable z = x +jy, and the systems of curves ф'(%, у, t) = const and ip'(x, y, t) = const are orthogonal, w is the complex acceleration potential.

The boundary condition at infinite distance from the airfoil is that u’, v’ -> 0, as shown in § 12.6. That on the airfoil is the tangency of the flow to the solid surface. To express the latter condition mathematically, we may assume that during oscillation every point of the airfoil moves in the vertical direction only. The velocity vector of a point on the airfoil is therefore vx = (0, dY/dt). The velocity vector of the fluid is v2 = (U + n’a, v’a) where the subscript a indicates that the corresponding quantities are evaluated on the airfoil. If we resolve these velocity vectors into directions tangent and normal to the airfoil, then the aforesaid boundary condition is that the normal components of vx and v2 must be equal. Now n = (— 3 Y/dx, 1) is a vector in the direction of the normal; hence, we must have vt • n = v2 • n, or, in terms of the components of these vectors,

ЗУ, rr, ЧЗУ,

— –(U+ua)— + va

Neglecting small quantities of the second order, we obtain the boundary condition

£У__ЭУ ЗУ Dt 3 t dx

Similarly, the normal components of the acceleration vectors of the fluid and the airfoil must agree. This leads to the boundary condition

An acceleration potential ф’ satisfying the boundary condition 8 does not necessarily satisfy the velocity boundary condition 7, which actually amounts to an additional restriction on </>’. To express Eq. 7 in terms of ф’, we have, from Eqs. 3,

For harmonic oscillations we may use the complex representation (§ 1.8) and write

Then

(И)

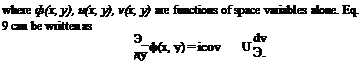Solving for v, and using the condition v = 0 when x = — oo, we obtain

ф:,у) = т, е-*«*™[Х (12)

U J – со ду

This must be equal to the right-hand side of Eq. 7 on the airfoil.*

In addition to the boundary conditions 7 and 8, the flow must also satisfy the Kutta-Joukowski condition that the velocity be finite at the trailing edge of the airfoil. An equivalent form of this condition is that the pressure (and hence ф) be continuous at the trailing edge of the airfoil.