DIMENSIONAL ANALYSIS OF THE FLUID DYNAMIC EQUATIONS
The governing equations that were developed in the previous section (e. g., Eq. (1.27)) are very complex and their solution, even by numerical methods, is difficult for many practical applications. If some of the terms causing this complexity can be neglected in certain regions of the flow field, while the dominant physical features are still retained, then a set of simplified equations can be obtained (and probably solved with less effort). In this section, some of the conditions for simplifying the governing equations will be discussed.
In order to determine the relative magnitudes of the various elements in the governing differential equations, the following dimensional analysis is performed. For simplicity, consider the fluid dynamic equations with constant properties (|U = const., and p = const.):
V-q = 0 (1.23)
p(|^ + 4* Vq) = pf-Vp + Iu V2q (1.30)
The first step is to define some characteristic or reference quantities, relevanl
to the physical problem to be studied:
L Reference length (e. g., wing’s chord)
V Reference speed (e. g., the free stream speed)
T Characteristic time (e. g., one cycle of a periodic process, or L/V)
p0 Reference pressure (e. g., free stream pressure, p„)
f0 Body force (e. g., magnitude of earth’s gravitation, g)
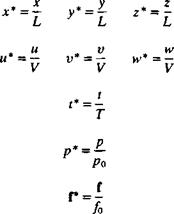 |
With the aid of these characteristic quantities we can define the following nondimensional variables:
If these characteristic magnitudes are properly selected, then all the non – dimensional values in Eq. (1.46) will be of the order of 1. Next, the governing equations need to be rewritten using the quantities of Eq. (1.46). As an example, the first term of the continuity equation becomes
Эи __ Эи ди* Эх* _V / du*
Эх ди* Эх* Эх Ldx*J
and the transformed incompressible continuity equation is
|
After a similar treatment, tl. e nomentum equation n the x direction becomes /Vdu* |
|
.V t du* |
|
I r w t, r „ „V Эи* ,V p{T~dF+vr ^+Vlv‘ ^ + VIW dz |
|
dy* Podp* ^ Pfofx L Эх* |
|
V (Э2и* д2и* д2и* – h—~r + |
![]()
V/Эи* dv* Эи»* _ Z 1аг* + эу*+ ~dz*!~
The corresponding equations in the у and z directions can be obtained by the same procedure. Now, by multiplying Eq. (1.47) by L/V and Eq. (1.48) by
L! pV2 we end up with
|
ди* „ Эи* л Эи* dt* + “ dx* + v dy* + w |
|
Эи* |
|
(Lfor* ( Po dP* V2)Jx pV2) Эх* |
![]()
Эи* dv* dw* Эх* + Э^* + ~9z*
![]() p Wd2!** З2и* aPu*^ ~pVL ) Эх*2 + Шу*2 + dz*2)
p Wd2!** З2и* aPu*^ ~pVL ) Эх*2 + Шу*2 + dz*2)
If all the nondimensional variables in Eq. (1.46) are of order 1, then all terms appearing with an asterisk (*) will also be of order 1, and the relative magnitude of each group in the equations is fixed by the nondimensional numbers appearing inside the parentheses. In the continuity equation (Eq.
(1.49) ), all terms have the same order of magnitude and for an arbitrary three-dimensional flow all terms are equally important. In the momentum equation the first nondimensional number is
![]() (1.51)
(1.51)
which is a time constant and signifies the importance of time-dependent phenomena. A more frequently used form of this nondimensional number is the Strouhal number where the characteristic time is the inverse of the frequency пі of a periodic occurrence (e. g., wake shedding frequency behind a separated airfoil),
![]() L wL (1 f(o)V = ~V
L wL (1 f(o)V = ~V
If the Strouhal number is very small, perhaps due to very low frequencies, then the time-dependent first term in Eq. (1.50) can be neglected compared to the terms of order 1.
The second group of nondimensional numbers (when gravity is the body force and ^ is the gravitational acceleration g) is called the Froude number, and stands for the ratio of inertial force to gravitational force:
![]() V
V
Wg
Small values of F (note that F~2 appears in Eq. (1.50)) will mean that body forces such as gravity should be included in the equations, as in the case of free surface river flows, waterfalls, ship hydrodynamics, etc.
The third nondimensional number is the Euler number, which represents the ratio between the pressure and the inertia forces:
![]()
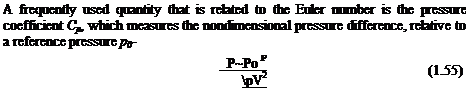 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
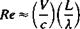
![]()
This formulation shows that the Reynolds number represents the scaling of the velocity-times-length, compared to the molecular scale.
The conditions for neglecting the viscous terms when Re»1 will be discussed in more detail in the next section.
For simplicity, at the beginning of this analysis an incompressible fluid was assumed. However, if compressibility is to be considered, an additional nondimensional number appears that is called the Mach number, and is the ratio of the velocity to the speed of sound a :
M = — (1.58)
a
Note that the Euler number can be related to the Mach number since p/p~a2 (see also Section 4.8).
Density changes caused by pressure changes are negligible if (see Karamcheti,15 p. 23)
M2 M2
M«1 ^«1 —«1 (1.59)
and if these conditions are met, an incompressible fluid can be assumed.











