VORTEX QUANTITIES

In conjunction with the velocity vector, we can define various quantities such as streamlines, stream tubes, and stream surfaces. Corresponding quantities can be defined for the vorticity vector that will prove to be useful later on in the modeling of lifting flows.

The field lines (e. g., in Fig. 2.2) that are parallel to the vorticity vector are called vortex lines and these lines are described by

t X d = 0 (2.46)

where d is a segment along the vortex line (as shown in Fig. 2.9). In cartesian coordinates, this equation yields the differential equations for the vortex lines:

dx _dy _dz

Z=Ty~Z

The vortex lines passing through an open curve in space form a vortex surface and the vortex lines passing through a closed curve in space form a vortex tube. A vortex filament is defined as a vortex tube of infinitesimal cross-sectional area.

The divergence of the vorticity is zero since the divergence of the curl of

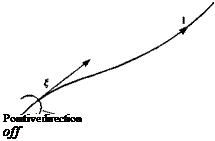FIGURE 2.9

Vortex line.

any vector is identically zero:

V-£ = V- VXq = 0 (2.48)

Consider, at any instant, a region of space R enclosed by a surface S. An application of the divergence theorem yields

[ l-ndS= f V-%dV = 0 (2.49)

Js Jr

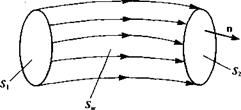
At some instant in time draw a vortex tube in the flow as shown in Fig. 2.10. Apply Eq. (2.49) to the region enclosed by the wall of the tube Sw and the surfaces Si and S2 that cap the tube. Since on Sw the vorticity is parallel to the surface, the contribution of Sw vanishes and we are left with

f £-ndS= f £-ndS+ f £-ndS = 0 (2.50)

Js Js, Js,

Note that n is the outward normal and its direction is shown in the figure. If we denote n„ as being positive in the direction of the vorticity, then Eq. (2.50) becomes

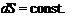
(2.51)

At each instant of time, the quantity in Eq. (2.51) is the same for any cross-sectional surface of the tube. Let C be any closed curve that surrounds the tube and lies on its wall. The circulation around C is given from Eq. (2.4) as

(2.52)

and is seen to be constant along the tube. The results in Eqs. (2.51) and (2.52) express the spatial conservation of vorticity and are purely kinematical.

If Eq. (2.52) is applied to a vortex filament and it,, is chosen parallel to the vorticity vector, then

Гc = £dS = const. (2.53)

and the vorticity at any section of a vortex filament is seen to be inversely proportional to its cross-sectional area. A consequence of this result is that a
vortex filament cannot end in the fluid since zero area would lead to an infinite value for the vorticity. This limiting case, however, is useful for the purposes of modeling and so it is convenient to define a vortex filament with a fixed circulation, zero cross-sectional area, and infinite vorticity as a vortex filament with concentrated vorticity.

Based on results similar to those of Section 2.3 and this section, the German scientist Hermann von Helmholtz (1821-1894) developed his vortex theorems for inviscid flows, which can be summarized as:

1. The strength of a vortex filament is constant along its length.

2. A vortex filament cannot start or end in a fluid (it must form a closed path or extend to infinity).

3. The fluid that forms a vortex tube continues to form a vortex tube and the strength of the vortex tube remains constant as the tube moves about (hence vortex elements, such as vortex lines, vortex tubes, vortex surfaces, etc., will remain vortex elements with time).

The first theorem is based on Eq. (2.53), while the second theorem follows from this. The third theorem is actually a combination of Helmholtz’s third and fourth theorems and is a consequence of the inviscid flow assumption (Eq. (2.9)).