THE STREAM FUNCTION

Consider two arbitrary streamlines in a two-dimensional steady flow, as shown in Fig. 2.17. The velocity q along these lines 1 is tangent to them

qx dl = иdz – wdx = 0

FIGURE 2.17

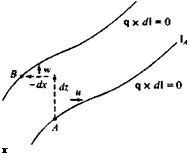Flow between two two-dimensional streamlines.

and, therefore, the flux (volumetric flow rate) between two such lines is constant. This flow rate between these two curves is

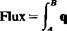•nd/= udz + w(—dx) (2.73)

‘a

where A and В are two arbitrary points on these lines. If a scalar function W(*, z) for this flux is to be introduced, such that its variation along a streamline will be zero (according to Eq. (1.5)), then based on these two equations (Eqs. (1.5) and (2.73)), its relation to the velocity is

Substituting this into Eq. (1.5) for the streamline results in

aw aw

dW = — dx+ — dz = dx dz

Therefore, dW along a streamline is zero, and between two different streamlines dW represents the volume flux (Eq. (2.73)). Integration of this equation results in

W = const. on streamlines Substituting Eqs. (2.74) into the continuity equation yields

Эи dw a2w a2w л

—- 1— —————— — 0

dx dz dx dz dx dz

and therefore the continuity equation is automatically satisfied. Note that the stream function is valid for viscous flow, too, and if the irrotational flow requirement is added then £y = 0. Recall that the у component of the vorticity

is

^_^=V2ip

dz dx
and therefore for two-dimensional incompressible irrotational flow V satisfies Laplace’s equation

V2V = 0 (2.78)

It is possible to express the two-dimensional velocity in the x-z plane as

34» ЗУ

— i – — k=jXV4»

dz dx

Thus

q=jxVW (2.79)

Using this method, the velocity in cylindrical coordinates (for the r-d) plane is obtained:

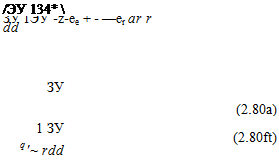q=j *

and the velocity components are

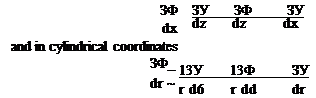The relation between the stream function and the velocity potential can be found by equating the expressions for the velocity components (Eq. (2.20) and Eq. (2.74)), and in cartesian coordinates:

These are the Cauchy-Riemann equations with which the complex flow potential will be defined in Chapter 6.

Laplace’s equation in polar coordinates, expressed in terms of the stream function, is

32У 1ЭУ 1 32У dr2 + r dr + r2 dd2

To demonstrate the relation between the velocity potential and the stream function, recall that along a streamline

dy = udz — wdx = Q

and similarly, along a constant potential line

d<& = udx + w dz = Q (2.85)

Since the slopes of the streamlines and the potential lines are negative reciprocals, these lines are perpendicular to one another at any point in the flow.