CONSTANT-STRENGTH SINGULARITY SOLUTIONS (USING THE NEUMANN BOUNDARY CONDITION)
A more refined discretization of a continuous singularity distribution is th6 element with a constant strength. This type of element is shown schematically in Fig. 11.16, and it is assumed that s j
![]()
 |
■—і—Ґ
X2 X *l*i
and as (x2 — xj—>0 the approximation seems to improve. In this case, only one constant (the strength of the element) is unknown and by dividing l
FIGURE 11.16
Constant-strength singularity approximation for a continuous strength distribution.
surface into N panels and specifying the boundary conditions on each of the collocation points, N linear algebraic equations can be constructed.
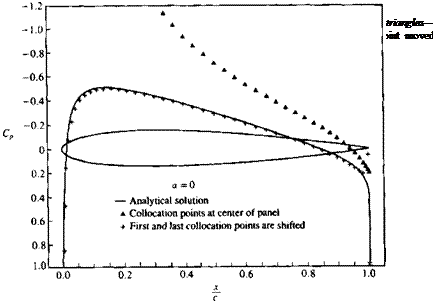
In principle, the point singularity methods are satisfactory in estimating the zero-thickness camberline lift, but are inadequate near the stagnation points of a thick airfoil. The constant-strength methods are capable of more accuracy near the stagnation points and can be used to model closed surfaces with thickness resulting in a more detailed pressure distribution, which is essential for airfoil shape design.











