Ceiling

This process of improving performance at altitude cannot be continued indefi­nitely and we shall eventually reach such a height that there is only one possible speed for level flight and the rate climb is nil. This is called the ceiling.

It requires extreme patience and time to reach such a ceiling, and, owing to the hopeless performance of the aeroplane when flying at this height, it is of little use for practical purposes, and therefore the idea of a service ceiling is introduced, this being defined as that height at which the rate of climb becomes less than 0.5 m/s, or some other specified rate.

Effect of weight on performance

It is sometimes important to be able to calculate what will be the effect on per­formance of increasing the total weight of an aeroplane by carrying extra load. Here again the performance curves will help us.

If the weight is increased, the lift will also have to be increased. So we must either fly at a larger angle of attack or, if we keep the same angle of attack, at a higher speed. This speed can easily be calculated thus –

Let old weight = W, new weight = Wv

Let У be the old speed, and Vj be the new speed at the same angle of attack. Since angle of attack is the same, CL will be the same.

.-. w = CL. ipV2 . s

and Wj = CL. ip Уj2 . S

so У/У = V(Wj/W)

Such problems always become more interesting if we consider actual figures; so suppose that we wish to carry an extra load of 10 000 N on our aeroplane which already weighs 50 000 N; then –

У/У = V(60 000/50 000) = Vl.2 = 1.095

Since the angle of attack is the same, the lift/drag ratio remains constant, and the corresponding drag, D, will be

D. = Db. = D X 65 000 = 1.2D 1 i 50 000

The corresponding power, P, is thus:

P1 = D1V1 = 1.2 X 1.095DL = 1.2P

So, for example, if we take the point on the power-required curve (Fig. 7.4) marked A, the corresponding point A, will be at

Vj = 1.095У, P1 = 1.2P

i. e. Vj = 1.095X 60 = 65.7m/s

and P1 = 1.2 X 310 = 372 kW

In a similar way, for each angle of attack, new speed and new power can be calculated, and thus a new curve of power required can be drawn for the new weight of the aeroplane.

It is interesting to note that the net effects of the additional weight are exactly the same as the effects of an increase of altitude, i. e. –

1. Slight reduction in maximum speed.

2. Large reduction in rate of climb.

3. Increase in minimum speed.

In short, the curve of power required is again displaced upwards. It will be noticed that there is too a slight increase in the best speed to use for climbing. (This must not be confused with rate of climb.)

In spite of the similarity in effect of increase of weight and increase of alti­tude it should be noted that the increase of weight does not affect the reading of the air speed indicator, and so the results apply equally well whether we consider true or indicated air speed.

The problems of operating piston engines at increasing altitude are such that their use is nowadays normally limited to flight at relatively low altitudes. This means that the piston engine is now relegated to use for light general avi­ation and specialist purposes. For propeller propulsion at higher altitudes and speeds, gas-turbine based turboprop propulsion is more appropriate, because the efficiency of the engine is less affected by altitude. The problem of pro­peller efficiency at high speed has been addressed with some success in recent years, and with very advanced propellers, it is indeed possible to fly even at transonic speeds. High-speed propellers are characterised by swept tips, giving a scimitar shape. The efficiency of propeller propulsion is theoretically greater than that of a pure jet, and for this reason, the turboprop is widely used for applications such as small regional airliners, transport aircraft and military trainers, where flight at very high altitude and speed is not necessary. Despite the advantages in terms of fuel consumption, the use of propellers does add to the weight, cost, complexity and servicing requirements.

Influence of jet propulsion on performance

In this chapter, we have so far looked at the performance of propeller driven aircraft, and it is now time to consider the effects of using turbojet propulsion. In Chapter 5 we saw that for the jet engine, thrust and fuel consumption do not change much with speed, and therefore the speeds for optimum range and endurance at any fixed altitude are faster than for a propeller driven aircraft with the same airframe. Also, as explained earlier in this chapter, by flying higher we will fly faster for a given amount of drag and thrust. This means that the optimum speeds for range and endurance also increase with altitude. Fortunately, the efficiency of the jet also rises with altitude, and we find that with turbojet propulsion, not only do the optimum speeds increase with height, but the number of kilometres that we can fly for each kilogram of fuel increases. Thus, for a jet aircraft, it is advantageous in terms of range, endurance and fuel cost to fly high and fast (Fig. 7C, overleaf). The limitation on maximum speed is normally provided by the onset of serious compress­ibility effects: transonic flow, which is dealt with in Chapter 11. The feature of obtaining the best economy at high speed is one reason for the popularity of jet propulsion for airliners, where passengers naturally want to get to their destinations as quickly and cheaply as possible. Other advantages are the low noise in the cabin, and the lack of vibration.

When considering the performance of jet aircraft, it is important to appreciate some important differences between the way that jet and piston – engined aircraft are controlled. On a piston-engined aircraft, the pilot controls the engine power by means of the throttle control, so called, because it tra­ditionally controlled the air flow into the engine by throttling it. On a jet aircraft, the pilot controls the engine by adjusting the fuel flow, and it is the thrust that is controlled directly, rather than the power. Despite the fact that this control does not actually throttle anything, it still tends to be called the throttle, for historic reasons.

Another difference between piston and jet propelled aircraft is that the higher speed of the latter means that the speed relative to the speed of sound becomes very important. For jet aircraft performance estimates, therefore, we need to display the data in a different form from that used for piston-engined aircraft. It is better to work in terms of thrust and drag rather than power required and power available, and we need to know how the thrust and drag vary with Mach number and altitude. This means that the simple performance calculations that we are able to use for practical purposes for low speed piston-engined aircraft are no longer appropriate for high-speed jet-engined aircraft. The proper method of dealing with their performance is rather com­plicated and beyond the intended level of this book, but in the numerical questions associated with this chapter, we have included some simple calcula­tions for jet aircraft at low speeds where compressibility effects can be ignored.

Can you answer these?

1. ‘When an aeroplane is climbing, the lift is less than the weight.’ Explain why this statement is not so inconsistent as it sounds.

2. What is the effect of altitude on the maximum and minimum speeds of an aeroplane?

3. Distinguish between ‘ceiling’ and ‘service ceiling’.

4. In attempting to climb to the ceiling, should the air speed be kept constant during the climb?

5. If the load carried by an aeroplane is increased, what will be the effects on performance?

For solutions see Appendix 5.

Numerical examples on Performance will be found in Appendix 3.

Fig 7C Cruise performance (opposite)

(By courtesy of the Boeing Company)

Two models of the Boeing 747. The nearer aircraft is a 747-400 which cruises at around 965 km/h (600 mph) at 9150 m, and has a cruise range of 13 528 km with 412 passengers.

In a sense, any motion of an aeroplane may be considered as a manoeuvre. In no other form of transport is there such freedom of movement. An aeroplane may be said to have six degrees of freedom which are best described in relation to its three axes, defined as follows –

The longitudinal axis (Fig. 8.1) is a straight line running fore and aft through the centre of gravity and is horizontal when the aeroplane is in ‘rigging position’.

The aeroplane may travel backwards or forwards along this axis. Backward motion – such as a tail-slide – is one of the most rare of all manoeuvres, but forward movement along this axis is the most common of all, and is the main feature of straight and level flight.

Any rotary motion about this axis is called rolling.

The normal axis (Fig. 8.1) is a straight line through the centre of gravity, and is vertical when the aeroplane is in rigging position. It is therefore at right angles to the longitudinal axis as defined above.

The aeroplane may travel upwards or downwards along this axis, as in climbing or descending, but in fact such movement is not very common, the climb or descent being obtained chiefly by the inclination of the longitudinal axis to the horizontal, followed by a straightforward movement along that axis.

Rotary motion of the aeroplane about the normal axis is called yawing.

The lateral axis (Fig. 8.1) is a straight line through the centre of gravity at right angles to both the longitudinal and the normal axes. It is horizontal when the aeroplane is in rigging position and parallel to the line joining the wing tips.

The aeroplane may travel to right or left along the lateral axis; such motion is called sideslipping or skidding.

Rotary motion of the aeroplane about the lateral axis is called pitching.

These axes must be considered as moving with the aeroplane and always remaining fixed relative to the aeroplane, e. g. the lateral axis will remain par­allel to the line joining the wing tips in whatever attitude the aeroplane may

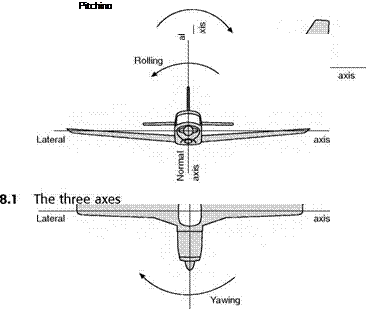be, or, to take another example, during a vertical nose-dive the longitudinal axis will be vertical and the lateral and normal axes horizontal.

So the manoeuvres of an aeroplane are made up of one or more, or even of all the following –

1. Movement forwards or backwards.

2. Movement up or down.

3. Movement sideways, to right or left.

4. Rolling.

5. Yawing.

6. Pitching.

Some of these motions, or combinations of motion, are gentle in that they involve only a state of equilibrium. These have already been covered under the headings of level flight, gliding, climbing, and so on. In this chapter we shall deal with the more thrilling manoeuvres, those that involve changes of direction, or of speed, or of both – in other words, accelerations. In such manoeuvres the aeroplane is no longer in equilibrium. There is more thrill for the pilot; more interest, but more complication, in thinking out the problems on the ground (Fig 8A).