Approaching the speed of sound

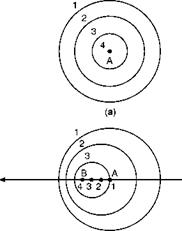
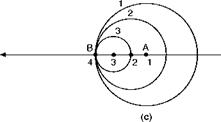
Consider a point A sending out pressure waves. If the point is not moving, suc­cessive waves 1, 2, and 3 will form circles round the point just like the waves which radiate from a point on the surface of water when a stone is dropped into the water at that point (Fig. 11.2a). Now suppose that the point A is moving in the direction shown, but at a speed less than the speed of propa­gation of the waves, and that it sends out the wave 1 when it is Al, 2 at A2, 3 at A3; the picture will now take the form of Fig. 11.2b. Now increase the speed of A until it is the same as the speed of the propagation of the waves (Fig. 11.2c), and we soon see why the air ahead gets no warning that A is approaching – we get a pretty good idea too how the waves pile up and what causes the ‘shock’.

Some time ago this ‘shock’, which occurred before the speed of sound was actually reached, and which in some instances had rather alarming effects on the flight of the aeroplane, was considered as something to be avoided at all costs; and the rapid increase in drag seemed a formidable enough ‘barrier’ at that time, if only because there seemed little hope of providing engine power to match it.

Thus it was that the transonic range of speeds, and especially the approach to the speed of sound, came to acquire rather a bad reputation in the minds of both designers and pilots, and the difficulty in solving the problems was all the more frustrating because we knew, from experience of the flight of bullets and shells, that flight beyond the speed of sound, flight at supersonic speeds, was not only possible but apparently free from some of the troubles of transonic flight.

To-day, of course, we know a great deal more about flight at transonic speeds, the ‘shock’ and the ‘barrier’ are no longer obstacles to be avoided but rather to be got over, or through, and the supersonic region is within the reach of aeroplanes as well as bullets and shells; but with all our increase of

(b)

Fig 11.2 Propagation of pressure waves

(a) Point stationary – sending out pressure waves 1, 2, 3, 4.

(b) Point moving below speed of sound.

(c) Point moving at the speed of sound.

knowledge, it is interesting to note that flight at transonic speeds still pres­ents special problems of its own. That is why it deserves a whole chapter to itself.