Mach angle

Figure 11.2 illustrated the piling up of the air in front of a body moving at the speed of sound, and explained how the incipient shock wave is formed. This incipient shock wave is at right angles to the direction of the airflow, and this means as near as matters at right angles to the surface of a body such as a wing.

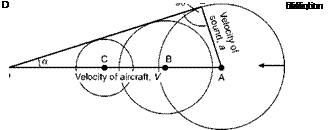
Now suppose a point is moving at a velocity У (which is greater than the speed of sound) in the direction A to D (Fig. 12.1). A pressure wave sent out when the point is at A will travel outwards in all directions at the speed of sound; but the point will move faster than this, and by the time it has reached D, the wave from A and other pressure waves sent out when it was at В and C will have formed circles as shown in the figure, and it will be possible to draw a common tangent DE to these circles – this tangent represents the limit to which all these pressure waves will have got when the point has reached D.

Now AE, the radius of the first circle, represents the distance that sound has travelled while the point has travelled from A to D, or, expressing it in veloc­ities, AE represents the velocity of sound – usually denoted by a – and AD represents the velocity of the point У.

Speed of point _ V Speed of sound a

(as illustrated in the figure this is about 2.5).

The angle ADE, or a, is called the Mach Angle and by simple trigonometry it will be clear that

in other words, the greater the Mach Number the more acute the angle a. At a Mach Number of 1, a of course is 90°.

Fig 12.1 Mach angle

If the moving point is a solid 3-dimensional body, such as a bullet, a com­plete cone – called the Mach Cone – will be formed, the angle at the apex being 2a. If the moving point represents a straight line such as the leading edge of a wing, a wedge will be formed, again with an angle 2a at the leading edge.

The tangent line DE is called a Mach Line, and it clearly represents the angle at which small wavelets are formed; the velocity of the airflow can even be calculated by measuring the angle on photographs of the wavelets.

Again the hydraulic analogy may be useful, since similar effects are seen when a ship passes through water or a thin stick is placed in a fast-moving stream of water. Only the region within the wedge formed by the bow waves is affected by the stick; the water outside this region flows on as if nothing was there. And the faster the flow, the sharper is the angle of the wedge.

It might be thought that the Mach Line represented the inclination of the shock waves – but this is not so. Disturbances of small amplitude travel at the speed of sound, but shock waves, which are waves of larger amplitude, actu­ally travel slightly faster than sound, and therefore they form at a rather larger angle to the surface. This fact is difficult to explain without going into the mathematics of fluid flow, which is quite beyond the scope of this book, but the following explanation of how shock waves are formed may help us to understand how their slope is determined.

Imagine a supersonic flow of air over a flat surface. This surface can never be perfectly smooth, and may be considered as consisting of a very large number of particles or slight bumps. At each of these bumps a Mach Line will be formed; its angle to the surface depending on the speed of the flow in accor­dance with the formula sin a = 1/M.

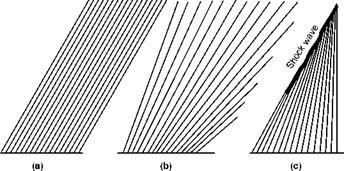
If the speed of flow remains constant, the Mach Lines will all be parallel as in Fig. 12.2a (overleaf).

If the speed of flow is accelerating, the Mach Lines will diverge as the angle becomes more acute with the increasing speed (Fig. 12.2b).

But if the speed of flow is decelerating the Mach Lines will converge, add up as it were, and form a more intense disturbance or wave, one of greater amplitude (Fig. 12.2c).

This is one way of explaining how a shock wave is formed at all, but it also gives some indication of how its slope is determined. Unfortunately it is not very convincing from this point of view, and it could even be argued that the slope of the shock wave is less steep than some of the Mach Lines. Also, is a shock wave formed because the air is slowing up, or is it the shock wave that slows up the flow?

Fig 12A Flight at supersonic speed (opposite)

(By courtesy of the Lockheed-California Company, USA)

The SR-71 Blackbird was capable of flight at Mach numbers in excess of 3. Delta wings with high leading-edge sweep, lifting chines on the forward fuselage, and two turbo-ramjet engines: bypass turbojets that effectively function as ramjets in high-speed flight.

Fig 12.2 Mach lines and shock wave

(a) Speed of flow constant.

(b) Accelerating flow.

(c) Decelerating flow.

So perhaps we must fall back on the argument that shock waves travel faster than sound, and even more on the fact that the shock wave is at a steeper angle than the Mach Lines, for very fortunately that it is a fact can easily be seen on photographs; e. g. in Fig. 11B it is clear that the bow and tail main shock waves are at a coarser angle than the small wavelets which result from small pressure disturbances due to the surface roughness.

Other examples of the practical effect of large disturbances travelling faster than the speed of sound are the hearing of sonic bangs before the noise of the aircraft, and the way in which the shock wave of an explosion is followed by the other noises.

But has all this got any practical significance in aircraft design? Yes, as a matter of fact, it has; but to understand what the practical significance is we must study the nature of supersonic flow.