Aerofoil data
The aerofoil sections, of which particulars are given in the following pages, have been chosen from among the thousands that have been tested, as being typical of the best that have been designed for particular purposes.
Although the values have been taken from standard tests, they have been modified so as to bring them as far as possible into line with each other, and simplified so as to correspond with the symbols and methods used in this book. In thus modifying the figures the aim has been to bring out the principles even at the sacrifice of some degree of accuracy. For the purpose of this book nothing is lost by this simplification and, while it is right and proper that official results should be given to the accuracy with which they can be measured, the student should remember that they are, after all, taken from experimental figures and that there is a limit not only to the accuracy of such figures, but even more so to the various corrections that have to be applied to them.
Unfortunately it is not possible to obtain results for all the sections at the same Reynolds Number, but for each the approximate Reynolds Number of the test has been given, and where alternative results are available those at the highest Reynolds’ Number have been chosen.
For reasons of security it is not possible to give test results for the most modern high-speed sections; but, even if they could be given, it is doubtful whether the tests would have been made at sufficiently high Mach Numbers and Reynolds Numbers to be reliable as a guide to full-scale performance. There is no difficulty in getting lift from bi-convex or double-wedge sections used at supersonic speeds, the problem is to keep down the drag.
For the benefit of those readers who would like to sketch out the shapes of the various aerofoil sections, the co-ordinates of the upper and lower surfaces are given; the measurements are expressed as percentages of the chord, negative values being below the chord line and positive values above it.
The tables give values of CL and CD at various angles of attack – from negative angles to above the stalling angle – but unfortunately values of CD are not available for aerofoils with flaps down (except for No. 8, the model of the Tightning). When a dash appears in the data columns it means that the figure
is not available, or that for some reason it would be meaningless. Pitching moments are given about the leading edge, or about the quarter-chord, or about the aerodynamic centre; and an opportunity is given in the short questions that follow the data for the reader to work out one from the other. Similarly the position of the centre of pressure can be found from other data, the lift/drag ratio from C£ and CD, and so on.
Most of the questions can be answered from the information given in Chapter 3, but the student may require a little guidance on the questions dealing with moment coefficients and centres of pressure, especially since the simplest method of reaching some of the answers is through the notation of differential calculus which has not been used in the text of the book.
For instance, to solve question (c) for RAF 15 (without slot):
In Chapter 3 when discussing the aerodynamic centre we arrived at the equation –
x/c = (CM. AC – Cm. le)/Cl (!)
or
CM. AC = CM. LE + Ш ■ CL (2)
By differentiating (2) with respect to CL we get the differential equation –
^^M. Ac/^L ~ ^M. LE^^L X^C (3)
But, by definition, the moment coefficient about the aerodynamic centre does not change with the angle of attack (or with the lift coefficient), or expressed in mathematical terms –
dCu. AC/dCL = 0
Therefore
x/c = – dCMLE/dCL (4)
By drawing a graph of CM LE against CL we can determine the slope of the curve, i. e. dCMLE/dCL for any value of CL, and so for any angle of attack. Thus we can get x/c from (4), and substitute in (2) to get CMAC. To solve question (c) for RAF 15 (with slot), we must first find CML£ from another formula in Chapter 3 –
CP position = —CML£/CL (5)
and then use the same method, as outlined above, to find CMAC. The same method can be used to solve questions (a) and (b) on the Clark YH aerofoil; and for questions (b) and (c) on NACA 0009 we can start from –
x’ = CMCI4/CL as in (5) above.
Finally it should be noted that formulae (1) and (2) are approximations based on the assumption that the angle of attack is small. The answers given in Appendix 4 have been arrived at by using these simplified formulae.
The more refined formula for (2) is –
CMAC = CMLE + x/c (CL cos a + CD sin a)
and the student is advised to work out one or two of the examples at the larger angles of attack with this formula, if only to confirm that the use of the simplified formula is justified – at any rate for the angles of attack of normal flight.
When differentiating the full formula, it must be remembered that cos a, CD and sin a all vary with CL and so the appropriate mathematical techniques must be used; these involve drawing graphs of cos a, CD and sin a against CL, in order to determine d cos a ldCL, dCD/dCL and d sin a ldCL.
More extensive questions on aerofoils will be found in Appendix 3.
1. RAF 15 *1A. RAF 15 with slot
|
Chord line |
Tike Clark Y, used on many early types of aircraft.
Figures relate to aspect ratio of 6.
Reynolds Number of test 3.5 million; with slot 200 000.
Slot assumed to remain open at position giving maximum lift.
(a) What is the max. value of LID with slot? without slot?
(b) What is the stalling angle with slot? without slot?
(c) What is the value of CMAC at +4° with slot? without slot?
(d) What is the value of CLmax/CDmin with slot? without slot?
(e) What is the value of CL^/CD (without slot) at 4° and 8°?
|
Distance from LE, % chord |
Upper surface |
Lower surface |
|
0 |
1.50 |
1.50 |
|
1.25 |
3.14 |
0.76 |
|
2.5 |
3.94 |
0.50 |
|
5 |
5.00 |
0.18 |
|
7.5 |
5.37 |
0.02 |
|
10 |
6.09 |
0.02 |
|
15 |
6.67 |
0.18 |
|
20 |
6.96 |
0.53 |
|
30 |
6.94 |
1.02 |
|
40 |
6.63 |
1.02 |
|
50 |
6.13 |
0.71 |
|
60 |
5.52 |
0.33 |
|
70 |
4.79 |
0.06 |
|
80 |
3.91 |
0.04 |
|
90 |
2.81 |
0.21 |
|
95 |
2.17 |
0.32 |
|
100 |
0.94 |
0.94 |
|
Angle of attack |
cL |
cD |
r ^M. LE |
*CL |
*cD |
,fCP, fraction of chord |
|
-4° |
-0.14 |
0.014 |
-0.036 |
-0.27 |
0.120 |
– |
|
22° |
+ 0.02 |
0.008 |
-0.052 |
-0.12 |
0.075 |
– |
|
0° |
0.14 |
0.008 |
-0.090 |
+0.03 |
0.056 |
– |
|
+2° |
0.32 |
0.012 |
-0.130 |
+0.18 |
0.050 |
0.70 |
|
+4° |
0.46 |
0.020 |
-0.160 |
0.33 |
0.050 |
0.45 |
|
6° |
0.60 |
0.030 |
-0.200 |
0.47 |
0.053 |
0.39 |
|
8° |
0.76 |
0.044 |
-0.240 |
0.62 |
0.060 |
0.37 |
|
10° |
0.90 |
0.060 |
-0.280 |
0.76 |
0.070 |
0.36 |
|
12° |
1.04 |
0.070 |
-0.310 |
0.90 |
0.080 |
0.34 |
|
14° |
1.16 |
0.096 |
-0.330 |
1.05 |
0.100 |
0.32 |
|
15° |
1.22 |
0.110 |
-0.340 |
1.12 |
0.110 |
0.31 |
|
16° |
1.16 |
0.140 |
-0.350 |
1.21 |
0.120 |
0.31 |
|
18° |
1.02 |
0.210 |
-0.384 |
1.36 |
0.148 |
0.30 |
|
20° |
0.94 |
0.260 |
-0.390 |
1.51 |
0.175 |
0.30 |
|
24° |
– |
– |
– |
1.70 |
0.234 |
0.30 |
|
26° |
– |
– |
– |
1.76 |
0.270 |
0.30 |
|
28° |
– |
– |
– |
1.76 |
0.304 |
0.30 |
|
30° |
– |
– |
– |
1.64 |
0.344 |
– |
|
34° |
– |
– |
– |
1.30 |
0.430 |
– |
2. Clark YH
|
Chord |
||
|
line Excellent American general purpose aerofoil. Modifications of Clark Y have been used on many types of aircraft all over the world; Clark YH was one of the first of these modifications. Figures relate to aspect ratio of 6, and standard roughness. Reynolds Number of test 7 million. |
||
|
Distance from LE, % chord |
Upper surface |
Lower surface |
|
0 |
3.50 |
3.50 |
|
1.25 |
5.45 |
1.93 |
|
2.5 |
6.50 |
1.47 |
|
5 |
7.90 |
0.93 |
|
7.5 |
8.85 |
0.63 |
|
10 |
9.60 |
0.42 |
|
15 |
10.68 |
0.15 |
|
20 |
11.36 |
0.03 |
|
30 |
11.70 |
0 |
|
40 |
11.40 |
0 |
|
50 |
10.51 |
0 |
|
60 |
9.15 |
0 |
|
70 |
7.42 |
0.06 |
|
80 |
5.62 |
0.38 |
|
90 |
3.84 |
1.02 |
|
95 |
2.93 |
1.40 |
|
100 |
2.05 |
1.85 |
|
Angle of attack |
cL |
cD |
CP, fraction of chord |
r ^M. LE |
L/D |
|
24° |
+0.09 |
0.010 |
– |
+0.030 |
-10 |
|
22° |
+0.05 |
0.009 |
0.74 |
-0.010 |
+ 5.2 |
|
0° |
0.20 |
0.010 |
0.40 |
-0.046 |
19.3 |
|
2° |
0.36 |
0.015 |
0.32 |
-0.072 |
23.2 |
|
4° |
0.51 |
0.022 |
0.295 |
-0.116 |
23 |
|
6° |
0.66 |
0.033 |
0.285 |
-0.150 |
20.6 |
|
8° |
0.80 |
0.045 |
0.275 |
-0.184 |
17.7 |
|
10° |
0.94 |
0.062 |
0.27 |
-0.220 |
15.2 |
|
12° |
1.06 |
0.083 |
0.27 |
-0.244 |
13.3 |
|
14° |
1.21 |
0.103 |
0.27 |
-0.276 |
11.8 |
|
16° |
1.33 |
0.125 |
0.265 |
-0.320 |
11 |
|
18° |
1.43 |
0.146 |
0.265 |
-0.352 |
9.9 |
|
19° |
1.36 |
0.170 |
0.275 |
-0.356 |
8 |
|
20° |
1.26 |
0.211 |
0.29 |
-0.354 |
7 |
|
25° |
0.97 |
0.324 |
0.33 |
-0.354 |
2.9 |
|
30° |
0.81 |
0.430 |
0.37 |
-0.352 |
1.9 |
(a) What is CMAC at 0°, 4° and 8° for this aerofoil?
(b) Where is the aerodynamic centre of this aerofoil section?
(c) What is the stalling angle?
(d) What is the value of CLmax/CD min?
(e) What is the value of CL^/CD at 4° and 8°?
*3A. NACA 0009 with flap
|
|
A thin symmetrical section.
All figures relate to standard roughness.
Reynolds Number of test 6 million.
Position of aerodynamic centre 0.25 of chord from LE. *With 20 per cent split flap set at 60°.
|
Distance from LE, % chord |
Upper and lower surfaces % chord |
|
0 |
0 |
|
1.25 |
1.42 |
|
2.5 |
1.96 |
|
5.0 |
2.67 |
|
7.5 |
3.15 |
|
10 |
3.51 |
|
15 |
4.01 |
|
20 |
4.31 |
|
30 |
4.50 |
|
40 |
4.35 |
|
50 |
3.98 |
|
60 |
3.50 |
|
70 |
2.75 |
|
80 |
1.97 |
|
90 |
1.09 |
|
95 |
0.61 |
|
100 |
0 |
|
Angle of attack |
cL |
cD |
r Ч1С/4 |
*cL |
4lC/4 |
|
28° |
-0.88 |
0.022 |
0 |
+0.45 |
-0.200 |
|
26° |
-0.65 |
0.014 |
0 |
+0.68 |
-0.210 |
|
24° |
-0.45 |
0.011 |
0 |
+0.90 |
-0.216 |
|
22° |
-0.21 |
0.010 |
0 |
+ 1.09 |
-0.220 |
|
0° |
0 |
0.009 |
0 |
+ 1.29 |
-0.216 |
|
+2° |
+0.21 |
0.010 |
0 |
+ 1.38 |
-0.218 |
|
4° |
+0.43 |
0.011 |
0 |
+ 1.65 |
-0.222 |
|
6° |
+0.64 |
0.014 |
0 |
+ 1.78 |
-0.225 |
|
8° |
+0.85 |
0.018 |
0 |
+ 1.72 |
-0.230 |
|
10° |
+0.90 |
0.021 |
-0.002 |
+ 1.58 |
-0.275 |
|
12° |
+0.89 |
0.028 |
-0.004 |
– |
– |
|
14° |
+0.87 |
0.036 |
-0.012 |
– |
– |
(a) What is the value of CMAC (without flap)?
Is it the same at all angles, as it should be?
(b) What is the position of the CP (without flap) at +4°?
(c) What is the position of the CP (with flap) at +4°?
(d) What is the value of LID (without flap) at 2°, 6°, 10°?
(e) What is the stalling angle (i) without flap? (ii) with flap?
 |
*4A. NACA 4412 with flap
Medium thickness NACA 4-digit good all round section. All figures relate to standard roughness.
Reynolds Number of test 6 million.
Position of aerodynamic centre 0.246 of chord from LE. *With 20 per cent split flap set at 60°.
|
Distance from LE, % chord |
Upper surface |
Lower surface |
|
0 |
0 |
0 |
|
1.25 |
2.44 |
-1.43 |
|
2.5 |
3.39 |
-1.95 |
|
5.0 |
4.73 |
-2.49 |
|
7.5 |
5.76 |
-2.74 |
|
10 |
6.59 |
-2.86 |
|
15 |
7.89 |
-2.88 |
|
20 |
8.80 |
-2.74 |
|
25 |
9.41 |
-2.50 |
|
30 |
9.76 |
-2.26 |
|
40 |
9.80 |
-1.80 |
|
50 |
9.19 |
-1.40 |
|
60 |
8.14 |
-1.00 |
|
70 |
6.69 |
-0.65 |
|
80 |
4.89 |
-0.39 |
|
90 |
2.71 |
-0.22 |
|
95 |
1.47 |
-0.16 |
|
100 |
0 |
0 |
|
Angle of attack |
cL |
cD |
r ^M. AC |
*cL |
4lC/4 |
|
-8° |
-0.45 |
0.022 |
-0.097 |
+0.90 |
-0.287 |
|
-6° |
-0.23 |
0.014 |
-0.092 |
+ 1.12 |
-0.297 |
|
-4° |
-0.03 |
0.012 |
-0.092 |
+ 1.34 |
-0.302 |
|
-2° |
+0.20 |
0.010 |
-0.092 |
+ 1.56 |
-0.305 |
|
0° |
+0.38 |
0.010 |
-0.093 |
+ 1.75 |
-0.305 |
|
+2° |
+0.60 |
0.010 |
-0.095 |
+ 1.95 |
-0.305 |
|
4° |
+0.80 |
0.012 |
-0.098 |
+2.14 |
-0.305 |
|
6° |
+ 1.00 |
0.014 |
-0.100 |
+2.43 |
-0.302 |
|
8° |
+ 1.15 |
0.017 |
-0.100 |
+2.50 |
-0.300 |
|
10° |
+ 1.27 |
0.022 |
-0.095 |
+2.65 |
-0.290 |
|
12° |
+ 1.36 |
0.030 |
-0.092 |
+2.63 |
-0.275 |
|
14° |
+ 1.35 |
0.042 |
-0.092 |
– |
– |
|
16° |
+ 1.25 |
0.059 |
-0.095 |
– |
– |
(a) What is the value of CMC/4 (without flap) at 0° and 8°?
(b) Where is the CP (without flap) at these angles?
(c) What is the value of LID (without flap) at these angles?
(d) What is the stalling angle (i) without flap? (ii) with 60° flap?
(e) What is the value of CLmax/CD min (without flap)?
Medium thickness 5-digit section that has been much used. Low drag; maximum camber well forward.
All figures relate to standard roughness.
Reynolds Number of test 6 million.
Position of aerodynamic centre 0.241 of chord from LE.
|
Distance from LE, % chord |
Upper surface |
Lower surface |
|
0 |
0 |
0 |
|
1.25 |
2.67 |
-1.23 |
|
2.5 |
3.61 |
-1.71 |
|
5.0 |
4.91 |
-2.26 |
|
7.5 |
5.80 |
-2.61 |
|
10 |
6.43 |
-2.92 |
|
15 |
7.19 |
-3.50 |
|
20 |
7.50 |
-3.97 |
|
25 |
7.60 |
-4.28 |
|
30 |
7.55 |
-4.46 |
|
40 |
7.14 |
-4.48 |
|
50 |
6.41 |
-4.17 |
|
60 |
5.47 |
-3.67 |
|
70 |
4.36 |
-3.00 |
|
80 |
3.08 |
-2.16 |
|
90 |
1.68 |
-1.23 |
|
95 |
0.92 |
-0.70 |
|
100 |
0 |
0 |
|
Angle of attack |
cL |
cD |
r Ч1С/4 |
r ^M. AC |
|
-8° |
-0.60 |
0.020 |
-0.018 |
-0.013 |
|
-6° |
-0.43 |
0.014 |
-0.015 |
-0.013 |
|
-4° |
-0.25 |
0.011 |
-0.013 |
-0.014 |
|
-2° |
-0.08 |
0.010 |
-0.013 |
-0.016 |
|
0° |
+0.15 |
0.010 |
-0.012 |
-0.016 |
|
+2° |
+0.36 |
0.010 |
-0.010 |
-0.015 |
|
4° |
+0.55 |
0.011 |
-0.008 |
-0.014 |
|
6° |
+0.75 |
0.013 |
-0.010 |
-0.014 |
|
8° |
+0.96 |
0.016 |
-0.013 |
-0.016 |
|
10° |
+ 1.14 |
0.023 |
-0.014 |
-0.017 |
|
12° |
+ 1.23 |
0.032 |
-0.012 |
-0.017 |
|
14° |
+0.82 |
0.045 |
-0.013 |
– |
|
16° |
+0.77 |
0.065 |
-0.050 |
– |
(a) What is the value of LID for this aerofoil at 0°, 4°, 8°?
(b) Where is the CP at these angles?
(c) Where is the maximum thickness?
(d) What is the stalling angle?
(e) What is the value of CL^/CD at 2°, 4° and 6°?
|
|
Typical thick 5-digit section of the 230 series.
All figures relate to standard roughness.
Reynolds Number of test 6 million.
Position of aerodynamic centre 0.241 of chord from LE.
|
Distance from LE, % chord |
Upper surface |
Lower surface |
|
0 |
0 |
0 |
|
1.25 |
4.09 |
-1.83 |
|
2.5 |
5.29 |
-2.71 |
|
5.0 |
6.92 |
-3.80 |
|
7.5 |
8.01 |
-4.60 |
|
10 |
8.83 |
-5.22 |
|
15 |
9.86 |
-6.18 |
|
20 |
10.36 |
-6.86 |
|
25 |
10.56 |
-7.27 |
|
30 |
10.55 |
-7.47 |
|
40 |
10.04 |
-7.37 |
|
50 |
9.05 |
-6.81 |
|
60 |
7.75 |
-5.94 |
|
70 |
6.18 |
-4.82 |
|
80 |
4.40 |
-3.48 |
|
90 |
2.39 |
-1.94 |
|
95 |
1.32 |
-1.09 |
|
100 |
0 |
0 |
|
Angle of attack |
cL |
cD |
r Ч1С/4 |
r ^M. AC |
|
-8° |
-0.62 |
0.016 |
-0.018 |
-0.008 |
|
-6° |
-0.47 |
0.014 |
-0.010 |
-0.007 |
|
-4° |
-0.28 |
0.012 |
-0.008 |
-0.007 |
|
-2° |
-0.09 |
0.011 |
-0.005 |
-0.007 |
|
0° |
+0.12 |
0.010 |
-0.002 |
-0.007 |
|
+2° |
+0.33 |
0.011 |
-0.001 |
-0.007 |
|
4° |
+0.53 |
0.012 |
0 |
-0.007 |
|
6° |
+0.72 |
0.014 |
+0.002 |
-0.007 |
|
8° |
+0.90 |
0.016 |
+0.003 |
-0.007 |
|
10° |
+ 1.01 |
0.020 |
+0.004 |
-0.008 |
|
12° |
+ 1.06 |
0.028 |
+0.005 |
-0.008 |
|
14° |
+0.75 |
0.040 |
+0.002 |
– |
|
16° |
+0.68 |
0.060 |
-0.020 |
– |
(a) What is the maximum thickness? Where is it?
(,b) What is the value of LID at -4°, 0°, 4°, 8°, 12°?
(c) Where is the CP on this aerofoil at 2°, 4° and 6°?
(d) What is the stalling angle?
(e) What is the maximum lift coefficient?
*7A. NACA 65,-212 with flap
|
|
Typical of the NACA 6 series; medium thickness.
All figures relate to standard roughness.
Reynolds Number of test 6 million.
Position of aerodynamic centre 0.259 of chord from LE. *With 20 per cent split flap set at 60°.
|
Distance from LE, % chord |
Upper surface |
Lower surface |
|
0 |
0 |
0 |
|
0.5 |
0.970 |
-0.870 |
|
0.75 |
1.176 |
-1.036 |
|
1.25 |
1.491 |
-1.277 |
|
2.50 |
2.058 |
-1.686 |
|
5.00 |
2.919 |
-2.287 |
|
7.5 |
3.593 |
-2.745 |
|
10 |
4.162 |
-3.128 |
|
15 |
5.073 |
-3.727 |
|
20 |
5.770 |
-4.178 |
|
25 |
6.300 |
-4.510 |
|
30 |
6.687 |
-4.743 |
|
35 |
6.942 |
-4.882 |
|
40 |
7.068 |
-4.926 |
|
45 |
7.044 |
-4.854 |
|
50 |
6.860 |
-4.654 |
|
55 |
6.507 |
-4.317 |
|
60 |
6.014 |
-3.872 |
|
65 |
5.411 |
-3.351 |
|
70 |
4.715 |
-2.771 |
|
75 |
3.954 |
-2.164 |
|
80 |
3.140 |
-1.548 |
|
85 |
2.302 |
-0.956 |
|
90 |
1.463 |
-0.429 |
|
95 |
0.672 |
-0.040 |
|
100 |
0 |
0 |
|
Angle of attack |
cL |
cD |
r Ч1С/4 |
*cL |
4lC/4 |
|
-8° |
-0.68 |
0.020 |
-0.025 |
+0.58 |
-0.223 |
|
-6° |
-0.50 |
0.015 |
-0.026 |
+0.80 |
-0.230 |
|
-4° |
-0.33 |
0.013 |
-0.030 |
+ 1.03 |
-0.240 |
|
-2° |
-0.10 |
0.010 |
-0.033 |
+ 1.25 |
-0.250 |
|
0° |
+0.12 |
0.009 |
-0.035 |
+ 1.45 |
-0.260 |
|
+2° |
+0.35 |
0.010 |
-0.037 |
+ 1.63 |
-0.265 |
|
4° |
+0.55 |
0.011 |
-0.038 |
+ 1.80 |
-0.267 |
|
6° |
+0.80 |
0.015 |
-0.039 |
+ 1.87 |
-0.264 |
|
8° |
+0.95 |
0.023 |
-0.040 |
+ 1.83 |
-0.260 |
|
10° |
+ 1.07 |
0.035 |
-0.040 |
+ 1.70 |
-0.255 |
|
12° |
+ 1.06 |
0.050 |
-0.038 |
+ 1.48 |
-0.380 |
|
14° |
+ 1.01 |
– |
-0.035 |
– |
– |
(a) What is Смлс? Is it the same at all angles, as it should be?
(b) Where is the maximum thickness?
(c) What is the stalling angle (i) without flap? (ii) with 60° flap?
(d) What is the maximum value of L/D?
(e) What is the value of CLmax/CDmin (without flap)?
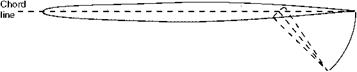
8. English Electric ASN/P1/3 *8A. English Electric ASN/P 1/3 with flap
|
|
This is the symmetrical aerofoil section used on the ВАС Mach 2+ Lightning. The wing was tapered and the ordinates relate to a section at 38.5 per cent of semi-span.
Reynolds Number of test 1.5 million (based on mean chord).
The values of coefficients refer to a complete model of the aircraft, not to the wing section alone.
The Lightning was a mid-wing monoplane with 60° sweepback on leading edge (see Fig. 11B).
*Model with approx 25 per cent plain flaps set at 50°.
|
Distance from LE, % chord |
Upper and lower surfaces % chord |
|
0 |
0 |
|
0.25 |
0.426 |
|
0.75 |
0.706 |
|
1.25 |
0.875 |
|
2.50 |
1.175 |
|
5.00 |
1.530 |
|
10 |
1.941 |
|
15 |
2.183 |
|
20 |
2.435 |
|
25 |
2.612 |
|
30 |
2.782 |
|
35 |
2.904 |
|
40 |
2.944 |
|
45 |
2.970 |
|
50 |
2.942 |
|
55 |
2.855 |
|
60 |
2.703 |
|
65 |
2.502 |
|
70 |
2.237 |
|
75 |
1.921 |
|
80 |
1.564 |
|
85 |
1.183 |
|
90 |
0.797 |
|
95 |
0.414 |
|
100 |
0.032 |
The values of CM are related to a point at 0.405 of mean chord. The position of the aerodynamic centre = 0.405 + dCM/dCL. The figures for the Tightning were given by courtesy of the former British Aircraft Corporation, Preston.
(a) What is the thickness/chord ratio of this aerofoil?
(b) Where is the maximum thickness?
(c) What is the stalling angle of the aircraft model: (i) with flaps up? (ii) with flaps down?
(d) What are the values of LID of the model at 4°, 12° and 20°: (i) with flaps up? (ii) with flaps down?
(e) What are the positions of the aerodynamic centre of the clean aircraft at 4°, 12° and 20°?
(Note: The answers involve the drawing of the curve of CM against CL and measuring the slopes of this curve at the specific angles.)
Data for ВАС Lightning model – clean aircraft
|
Angle of attack |
cL |
cD |
|
|
0° |
0 |
0.020 |
-0.017 |
|
2° |
0.08 |
0.020 |
-0.013 |
|
4° |
0.17 |
0.030 |
-0.008 |
|
6° |
0.27 |
0.040 |
-0.006 |
|
8° |
0.38 |
0.050 |
+0.005 |
|
10° |
0.50 |
0.075 |
+0.010 |
|
12° |
0.61 |
0.105 |
+0.016 |
|
14° |
0.71 |
0.140 |
+0.026 |
|
16° |
0.81 |
0.180 |
+0.040 |
|
18° |
0.91 |
0.225 |
+0.055 |
|
20° |
1.00 |
0.275 |
+0.070 |
|
22° |
1.09 |
0.335 |
+0.088 |
|
24° |
1.17 |
0.405 |
+0.108 |
|
26° |
1.22 |
0.480 |
+0.124 |
|
28° |
1.26 |
0.560 |
+0.132 |
|
30° |
1.27 |
0.650 |
+0.140 |
|
Data for ВАС Lightning model |
– flaps at 50° |
||
|
Angle of attack CL |
cD |
||
|
0° |
0.17 |
0.07 |
-0.072 |
|
2° |
0.27 |
0.07 |
-0.068 |
|
4° |
0.37 |
0.08 |
-0.062 |
|
6° |
0.47 |
0.09 |
-0.060 |
|
8° |
0.57 |
0.11 |
-0.053 |
|
10° |
0.67 |
0.13 |
-0.040 |
|
12° |
0.78 |
0.16 |
-0.032 |
|
14° |
0.88 |
0.20 |
-0.025 |
|
16° |
0.98 |
0.25 |
-0.015 |
|
18° |
1.07 |
0.31 |
+0.005 |
|
20° |
1.15 |
0.37 |
+0.013 |
|
22° |
1.22 |
0.43 |
+0.020 |
|
24° |
1.27 |
0.50 |
+0.037 |
|
26° |
1.27 |
0.55 |
+0.045 |
|
28° |
1.22 |
0.59 |
+0.074 |
|
30° |
1.16 |
0.63 |
+0.074 |