Induced Inflow Ratio
The induced inflow velocity, iy, at the rotor disk can be written as
Vh = Vi = Xh&R, _ (2.25)
where the nondimensional quantity X^ is called the induced inflow ratio in hover. The angular or rotational speed of the rotor is denoted by Q and R is the rotor radius; so the product is simply the tip speed, Vtjp, which is also sometimes given the symbol V^r. The inflow ratio is normally the preferable quantity to use when comparing results from different rotors because it is a nondimensional quantity. For rotating-wing aircraft, it is the convention to nondimensionalize all velocities by the blade tip speed in hovering flight (i. e., by Vtip = &R = VnR).
2.3 Thrust and Power Coefficients
Like all branches of engineering, nondimensional coefficients are normally employed in helicopter rotor analysis. Consider the induced velocity, vt, through the rotor. This can be written in functional form in terms of rotor thrust T, a reference area A such as disk area, a reference velocity V such as blade tip speed Vtip, and the density of the flow p using
Vi = fi(T, A, Vtip, P) or f2(T, A, Vtip, P, Vi) = 0. (2.26)
According to the Buckingham П method of dimensional analysis [see Anderson (2001)] this means there are five variables (N = 5), three fundamental dimensions (К = 3, namely: mass,
length, and time) and N — К = 2 or two П products. The functional dependence can, therefore, be written in the form
/з(ПьП2) = 0, – (2.27)
|
p-‘A’lVtr2T = |
|
MV2, |
where Пі and П2 are nondimensional groupings. Choosing the variables p, A, and VtjP as repeating variables (which are all linearly independent) the two nondimensional П products can each be written in terms of these repeating variables plus one other variable. Making each grouping dimensionally homogeneous, the first П product can be written as
which is a thrust coefficient. The second П product becomes
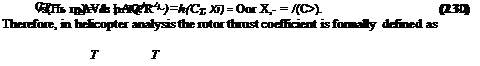 |
which is an inflow coefficient. This means that
where the reference area is the rotor disk area A and the reference speed is the blade tip speed, QR. This definition follows the one used by Glauert (1935). All velocity components are nondimensonalized by tip speed so the inflow ratio X,- is related to the thrust coefficient in hover by
This is based on the 1-D flow assumption made in the preceding analysis, which means that this value of inflow is assumed to be distributed uniformly over the disk. The rotor power coefficient is defined as
so that based on momentum theory the power coefficient for the hovering rotor is
Cp pA(ftR)3 (pA(QR)2) (ftf?) Сткі V2‘ (2‘34)
Again, this is calculated on the basis of uniform inflow and no viscous losses, so is called the ideal power coefficient. The corresponding rotor shaft torque coefficient is defined as
![]() 6^6
6^6
pAV2RR pAQ2R2′
Notice that because power is related to torque by P = QQ, then numerically Cp = Cq.
It is important to note that the US customary definition of the thrust, torque, and power coefficients is different to that used in some parts of the world (mainly in Britain, most of Europe, and Russia), where a factor of one half is used in the denominator giving
TO P
CT = —————- -, CQ = ———————– , and CP = ————————- -. (2.36
pA{&R)2 У ipA(£2R)2R ±pA(QR)3
This means that the values of thrust, torque, and power coefficients are all a factor of 2 greater than the values obtained with the US customary definition. The US definitions in Eqs. 2.31, 2.33, and 2.35 are used throughout this book.











