Momentum Analysis in Axial Climb and Descent

2.13.1 Axial Climb

Adequate climbing flight performance is an important operational consideration for a helicopter and sufficient power reserves must be available to ensure climbing per­formance is maintained over a wide range of gross weights and operational density al­titudes. Again, we can apply the three conservation laws to a control volume surround­ing the climbing rotor and its flow field, as shown in Fig. 2.17. As before, consider the problem to be quasi-1-D in that the flow properties will be assumed to vary only in the vertical direction over cross sectional planes parallel to the disk and at each cross section the flow properties are distributed uniformly. In contrast to the hover case where the climb velocity is identically zero, the relative velocity far upstream relative to the rotor will now be Vc. At the plane of the rotor, trie velocity will now be Vc + Vi, and the slipstream velocity

Figure 2.17 Flow model for momentum theory analysis of a rotor in axial climbing flight.

in the vena contracta is now Vc + w. By the conservation of mass, the mass flow rate is constant within the boundaries of the wake and so

m = JJ pV-dS = JJ^pV-dS, (2.71)

where dS is again the outward pointing normal from the control volume. Therefore, sub­stituting the values for this problem results in

m = pAoo(Vc + w) = pA(Vc + ы).

The application of the principle of conservation of momentum gives

T=jj p(V • dS)V – f f p(V ■ dS)V.

J J oo J Jo

Now, in a steady climb the velocity far upstream of the rotor is finite, so that both terms on the right-hand side of the above equation are nonzero. Therefore, in this case

T = m(Vc + w) — mVc = mw.

Notice that this is the same equation obtained for the rotor thrust in the hover case (Eq. 2.7). Because the work done by the climbing rotor is now T( VC + иг ), then

T(.vc + Vi) = II p(V-dS)V2- jjP(V-dSWi

= ^m(Vc + v})2 — jfflVc2 = lmu>( 2VC + u>). (2.75)

From these latter two equations, it is readily apparent that w = 2u,-, which is the same result as found for the hover case.

The relationship between the rotor thrust and the induced velocity at the rotor disk in hover is

and for the climbing rotor it has been shown from Eq. 2.74 that T = rirw — pA(Vc + Vi)w = 2 pA(Vc +

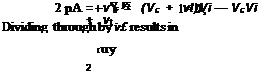so that

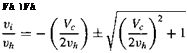which is a quadratic equation in v-Jvh. This equation has the solution

Although there are two possible solutions (one positive and one negative), гу /1v, must always be positive in the climb so as not to violate the assumed flow model. Therefore, the only valid solution becomes

(2.81)

The results from this analysis are shown in Fig. 2.18, which is presented in a form first suggested by Hafner (1947). The other root of the quadratic equation lies below the Vjvh axis and is physically invalid. It is apparent that as the climb velocity increases the induced velocity at the rotor decreases. This is called the normal working state of the rotor, with hover being the lower limit. The branch of the induced velocity curve denoted by the broken line gives a solution to Eq. 2.81 for negative values of Vc (i. e., a descent). However, just as the rotor begins to descend there can be two possible flow directions; this violates the assumed flow model and so this solution is also physically invalid. Yet the measurements follow closely this nonphysical root of the inflow equation, so in practice the momentum theory result can be assumed valid at least for low rates of descent.