Effects of Swirl Velocity

Before considering this optimum rotor, however, it is important to consider the significance of the wake swirl in determining the aerodynamic environment at the blade elements. For a helicopter the wake swirl is a function of rotor operating state (mainly thrust, as discussed on page 69), but swirl is generally small and practice has shown that for a helicopter the swirl can be ignored without any significant effects on predicted blade loads or rotor performance. The most complete and comprehensive exposition of the swirl effects on rotor performance is given by Glauert (1935), but Nikolsky (1951) also gives a good summary. In the generalized differential momentum theory, the thrust and torque on an annulus of the rotor in the hover state are, respectively,

dT=Anpvfydy and dQt — АжpviQ. a’yi dy, (3.87)

where a’ is known as the wake rotational interference factor. In terms of a’ the work done by the rotor over the annulus is

(l-a’)QdQi =vidT. (3.88)

In the case were the wake swirl is ignored (i. e., a’ = 0), then these results reduce to the two equations used previously, i. e.,

dT = 4лгpvfy dy and QdQi = dPt = 4npv? y dy.

In nondimensional form these are also the same as those used before, that is,

When the wake swirl is included, then the equations become

dCj — 4kfr dr

and

d. CPi = 4AfaV3 dr (3.92)

and with the additional equation

(1 – a’)a’r2 = к]. (3.93)

These are the equations of Glauert’s generalized differential momentum theory.

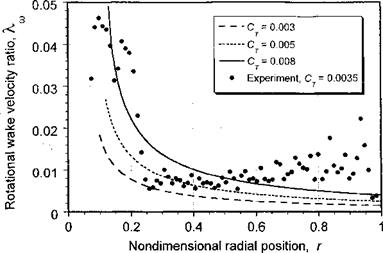
To illustrate the relative magnitude of the induced swirl for a helicopter, it is convenient to assume that A, is distributed uniformly as in the ideal case, in which case Eq. 3.93 can be solved for a’. Results are shown in Fig. 3.10 for several representative rotor-thrust coeffi­cients. The nondimensional swirl velocity Xw is simply a’r. Time-averaged measurements made in the wake of a two-bladed hovering rotor are also shown and, while there is signif­icant scatter because of the low velocities being measured, the magnitude and distribution are in general agreement with the theory. Notice that the swirl values are small over a large part of the blade (less than 2% of tip speed) but increase more rapidly toward the blade root. This region, however, is of little importance aerodynamically. There is some increase in swirl velocity near the blade tip, which is part of the signature of the tip vortex. Therefore, as a contributor to the resultant velocity and AoA at the blade element it is clear that the effects of the swirl in defining the aerodynamic environment for a helicopter rotor is small, but not completely negligible.