Center of Pressure
As shown previously by means of Fig. 7.15, the net aerodynamic loads on an airfoil may be represented by a normal force, an axial force (leading edge suction or chord force), and a pitching moment. For each value of the normal force a single point can be determined about which the pitching moment is zero. Therefore, the loading on the airfoil can be replaced only by normal and axial (chord) forces acting at this point, which is called the center of pressure. The aerodynamic center is a fixed point on the airfoil at a given Mach number and below stall, but the center of pressure moves to different locations on the chord with changes in AoA. For example, we may find the center of pressure, xcpj on an airfoil using the normal force and pitching moment about the 1/4-chord. Using Fig. 7.20 with xa = с/4 and x = xcp, we take moments about the leading edge to obtain
![]()
![]() Mie = (Mi/4 — Л/) – = —Nxcp, and in coefficient form this becomes
Mie = (Mi/4 — Л/) – = —Nxcp, and in coefficient form this becomes
— С ( I – jc
‘m i/4 — ‘-‘и ^ лср
so that the center of pressure is given by
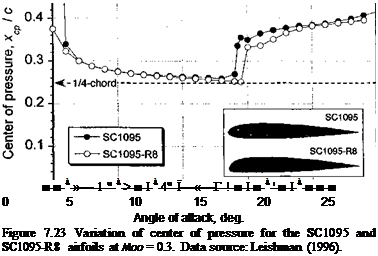
The coefficient Cmi/4 is generally negative, so that the center of pressure will be behind the aerodynamic center. This effect is shown in Fig. 7.23, where it will also be noticed that the center of pressure moves forward and approaches the aerodynamic center (which is near 1 /4-chord) for higher values of Cn, but below stall. After the airfoil stalls, the center of pressure stabilizes and approaches mid-chord. This reflects the form of the pressure distribution over the upper surface of the airfoil, which is much more uniform when the flow is separated.
 |
0.5
 |
Consider an example to illustrate the forgoing concepts of aerodynamic center and center of pressure. If the results of the lift coefficient and the pitching moment about 1/3-chord as a function of AoA are given in Table 7.3 then it is possible to determine the position of the aerodynamic center and the variation of the center of pressure as a function of AoA. In addition, it is possible to determine the lift-curve-slope, the zero-lift AoA and the zero-lift pitching moment.
By inspection, we see that the lift-curve-slope, C/a, is exactly 0.11 per degree. We can write a simple linear relationship for the lift-coefficient that Ci = C/a(a — ao) where a0 is the zero-lift angle. It is easy to determine ao from any known value of Q. For example, when a = 0 then from the table Q = 0.06 so that ao = —0.06/0.11 = —0.45°. By inspection, the slope of the Cm,/3 by a curve is exactly 0.01 per degree. We can find the zero-lift pitching moment coefficient by using the equation
Сч = С"”і-(‘^£)(“"“»>• (767)
Using the result, for example, that СШ|/3 = —0.01 when a = 0 gives that
CmQ = -0.01 – 0.01(0.0 – (-0.45)) = -0.0145. (7.68)
The position of the aerodynamic center can be found from the lift and pitching moment about any known point using Eq. 7.62. In this case, we use the equation
![]() 1 ZdCmi/3 1 ґ<1СтиЛ (da “ 3 ~~ V dci / 3 ~~ V da )dCi)
1 ZdCmi/3 1 ґ<1СтиЛ (da “ 3 ~~ V dci / 3 ~~ V da )dCi)
Substituting in the appropriate values leads to xac = 0.333 — 0.01/0.11 = 0.242. Finally, the center of pressure can be found from the equation
the results from which are given in Table 7.4. Notice again that the center of pressure comes closer to the aerodynamic center for larger values of Q (but below stall).











