Effects of Sweep Angle on Dynamic Stall
The local sweep or yaw angle of the flow to a blade element on a helicopter rotor in forward flight can be significant. The radial component of the velocity relative to the leading edge of the blade is the source of this sweep angle, as shown in Fig. 9.11. The sweep angle, A, is defined in terms of the normal and radial velocity components Ut and Ur, respectively, by
л(r, fr) = tan-1 (= tan-1 ( . (9.6)
Ut ) r + [Msmf J
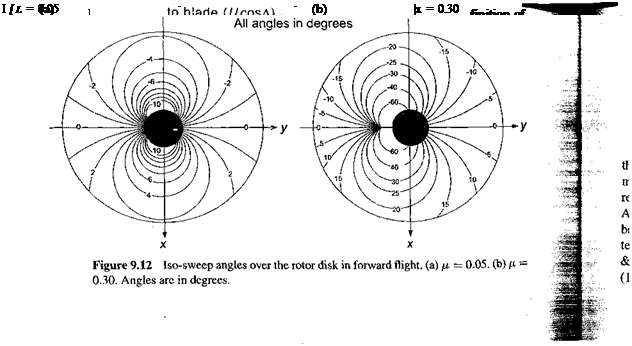
Examples of the iso-sweep angle distribution over the rotor disk are shown in Fig. 9.12 for advance ratios of 0.05 and 0.3. At the higher advance ratios, the sweep angles can exceed 30° over some parts of the disk. Overall they clearly become significant enough that their effects would need to be assessed experimentally by means of wind tunnel tests; any effects on the aerodynamics so produced will also need to be represented and properly integrated within a model of dynamic stall/
In the classical blade element theory, we usually neglect the effect of sweep on the lift, drag, and pitching moment. This is in accordance with the independence principle of sweep – see Jones & Cohen (1957). However, when an airfoil is operated at high AoA near stall this may not be a valid assumption. For example, the effect of sweep angle on the static lift characteristics of a swept 2-D airfoil is shown in Fig. 9.13. The results are based on the measurements of Purser & Spearman (1951) and are presented in the conventional blade element format – that is, in terms of AoA and velocities normal to the leading edge of
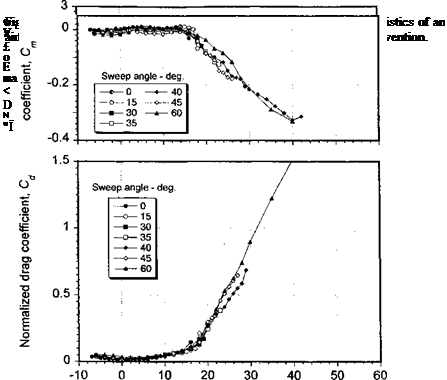 |
the airfoil section. When the data are presented this way, the results for the lift, pitching moment, and drag show a close correlation and confirm that, at least in the attached flow regime, the independence principle is a valid assumption. However, notice that in the high AoA region a much higher lift coefficient is obtained for the larger sweep angles. This is because of favorable effects on the spanwise development of the boundary layer, which tend to delay the onset of flow separation on the wing to a higher AoA – see also Dwyer & McCroskey (1971). Similar results have been found experimentally by St. Hillaire et al. (1979) and St. Hillaire & Carta (1979,1983a, b).
The upshot of these observations is that if these sweep effects are to be found on the rotor then they will tend to delay the onset of stall on the rotor to higher values of thrust, a result observed experimentally. Various earlier studies of the problem, including those of Harris (1966) and Gormont (1973), suggest that improvements in rotor thrust prediction can be obtained by including a static stall model that accounts for a delayed stall AoA and higher maximum lift as a function of sweep angle. However, it must be remembered that when stall occurs on the rotor in forward flight, the stall is actually dynamic in nature. To assess this problem, a series of experiments have been conducted by St. Hillaire & Carta (1979,1983a) where a NACA 0012 airfoil at a constant sweep angle of 30° was used.
These oscillating airfoil tests were perfoimcd at Mach numucis ui O. j and 0.4 and Reynolds numbers that are nominally full-scale rotor values. The measurements were determined by the integration of sectional pressures measured by pressure transducers distributed about a section at the mid-span of the model. Leishman (1989) has also conducted an analysis of these data. It appears that for fully attached unsteady flows the independence principle also applies. Any unsteady effects associated with sweep are small in the attached flow regime – probably smaller than uncertainties associated with the measurements themselves. However, in the dynamic stall regime, there are other characteristics of swept flow that are worthy of consideration.
|
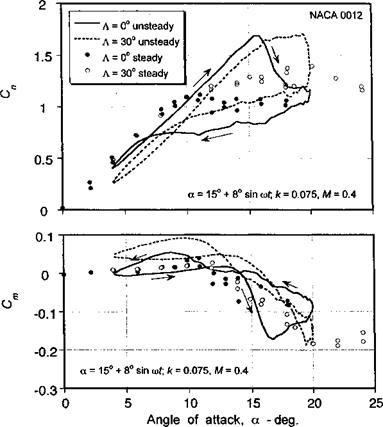
Figure 9.14 Behavior of the dynamic lift and pitching moment for a pitch oscillation in swept and unswept flow. |
Figure 9.14 shows a typical behavior of the lift and pitching moment coefficients in the dynamic stall regime for a pitch oscillation. A feature of these dynamic stall results is that compared with the static case where approximately a 20% higher maximum Cn was attained for A = 30°, the unsteady case shows a delay in dynamic lift stall to a higher AoA, but not to a significantly higher maximum value of lift. Also, for A = 30° somewhat narrower lift hysteresis loops are produced, and the mean value of lift is somewhat higher. Thus, it appears that the effects of sweep on the rotor may serve to provide an overall increase in average rotor thrust compared to predictions obtained when sweep effects are not included. It should be noted,, however, that the expected increase in thrust is not because of higher
![]() Knt cimnlv Краяне** thf* тмп vain*» nf tfiF* lift ie biahnr Thf* Hivprapnrp in
Knt cimnlv Краяне** thf* тмп vain*» nf tfiF* lift ie biahnr Thf* Hivprapnrp in
the pitching moment (moment stall) occurs at the same nominal value of AoA for both the A = 0° and A = 30° cases. However, the slope of the pitching moment curve during the next part of the cycle is clearly less for the A =30° case. Also, the minimum pitching moment is reached at a higher AoA. This suggests that the delay in dynamic lift stall to a higher AoA in swept flow is due, in part, to a lower velocity at which the shed leading edge vortex is convected over the chord. The comprehensive analysis performed on the airfoil pressure time histories by St. Hillaire & Carta (1983a) also supports this observation. In light of these results, it would appear that from a modeling perspective simple corrections to the stall AoA based on steady flow observations, such as suggested by Harris (1966), may give the desired effect on rotor performance predictions, but for the wrong underlying reasons. This problem, like several others in rotating-wing aerodynamics, illustrates the difficulties in simply extrapolating observations of quasi-2-D steady airfoil behavior to the complicated 3-D flow environment found on rotors.