Blade—Vortex Interactions (BVIs)

It will be apparent from the forgoing discussion that one of the distinctive features of rotor wakes in forward flight is the preponderance of potentially close interactions of blades and tip vortices, which are called blade-vortex interactions or BVIs. When viewed from above [i. e., see Fig. 10.8(a)] the trajectories formed by the tip vortices trace out closely epicycloidal forms. If the wake is assumed to be undistorted in the x-y (TPP) plane (a justifiable assumption near the rotor disk based on the example shown in Fig. 10.8), then the tip vortex trajectories are described geometrically by the parametric equations

= x’ti = cos(fb – fw) +

A

= >’tiP = sin(V9> – fw),

where is the position of the blade when the vortex was formed, and is the age of the vortex element relative to that blade (see Fig. 10.11). It has been assumed that no wake contraction occurs in the radial dimension.

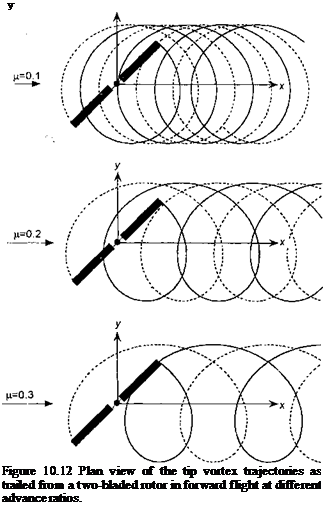
Examples of the wake topology when viewed from above the rotor are shown for three advance ratios in Fig. 10.12, with results for a two-bladed rotor being shown for simplicity. It will be apparent that BVIs can occur at many different locations over the rotor disk and also with different orientations between the blade axis and the vortex axis. If BVI occurs on the advancing side of the rotor disk, the blade and vortex axis can be nearly parallel. It has been described in Chapter 8 how these conditions promote (at least locally) highly

Figure 10.11 Definition of the position of an element in the vortex wake.

unsteady airloads on the blades, which can also be accompanied by significant obtrusive noise with strongly focused directivity – see Schmitz (1991). For a rotor with Nb blades, and assuming an undistorted wake, the locus of all the potential В Vis can be determined if the equations r cos (j/b – A) = cos(^ – + ktfw (10.3) and

r sin cjrb — A) = sin(V^ – fw) (10.4) are simultaneously satisfied for r (on the blade) and frb, where A = 2n(i — 1 )/Nb, і = 1,2,…, Nb with Nb as the number of blades and ifrw is the age of the vortex (wake age) relative to the blade from which it originated. It can be shown that for the blade positions

— cos A sin^u, — A) ± sin Ayjцїф-і — sin2Cirw — A)

(Ю.5)

and note that this is a multi-valued solution. We are only interested in the real parts (i. e., /х2і/^ — sin2(^w — Д) > 0) with particular attention to the signs of the angle and multiple values of the arcsine. The corresponding value of r is obtained from

sin(^fc – fw)

sinCV’fc – A)

where we are only interested in the disk itself (r < 1). Finally, the x, у locations of the ВVI intersection points over the disk are obtained from

x = r cos(фь — A) and у = r sin(xf/ь — Л). (10.7)

By solving for J/b and r for numerical values of yfrw > 0, we can determine all the locations of the potential BVI intersection points. (See also Questions 10.3 and 10.4.)

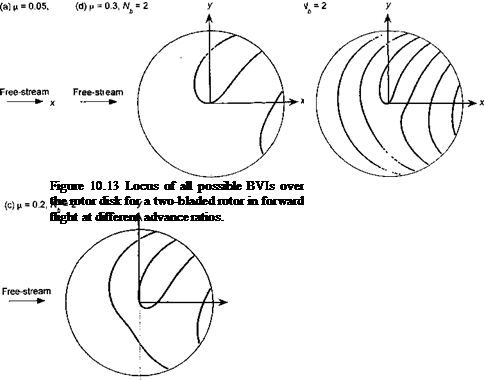Figure 10.13 shows these locations for a two-bladed rotor (AV== 2) operating in forward flight at four advance ratios. Again, it should be appreciated that this calculation assumes that all the vortices lie in the TPP. For any one flight condition they do not, but these figures give an indication of all the possible intersection locations. Notice that the largest number of potential BVIs occur in low speed forward flight. As forward speed increases, their number is reduced considerably. However, even though the number of potential interactions may decrease, it is their intensity and also the trace Mach number of the interaction that determines the potential noise and directivity of noise associated with а В VI – see Lowson (1996) and Leishman (1999), as well as Section 8.19.

Despite its importance to helicopter noise and vibration, clear experimental studies of the parallel BVI problem are relatively rare. Good, albeit idealized, quantitative measure­ments of blade vortex interactions and collisions are described by Horner et al. (1994) and Kitaplioglu & Caradonna (1994). Contributions to visualizing the problem have been achieved with the use of smoke [see Mercker & Pengel (1992) and Lorber et al. (1994)] and using strobed shadowgraphy [see Swanson (1993)].

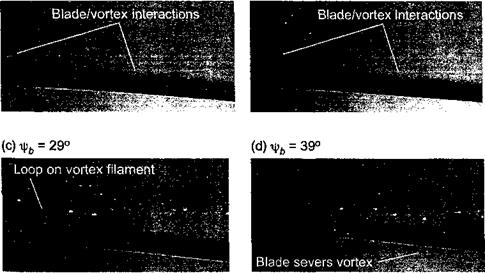
The other type of BVI occurs when the blade and vortex axes are almost perpendicular, which is mainly over the front and rear of the disk. While the former type tends to produce the largest unsteady airloads and noise generation, the latter tends to result in more highly 3-D airloads and broadband noise – see Schmitz (1991). Figure 10.14 shows a sequence of flow visualization images obtained with wide-field shadowgraphy, which detail the blades encountering a perpendicular type of BVI over the leading edge of the rotor disk during low-speed forward flight. We see that as the older wake vortices move downstream (to the right) they move up and over the top of the following blades (see also Fig. 10.13). A disturbance is produced on the older vortices as following blades pass underneath. After the blade passes, the tip vortices return to their original undisturbed shape. For progressively greater wake ages, the vortices are convected further downstream and the blade intersects and severs the vortex filament. This can result in an instability or transition bifurcation that is characterized by a large growth in the viscous core dimensions. This is known as “vortex bursting,” although the proper explanation of this phenomenon perhaps remains somewhat controversial. However, an increase in the effective core size and/or diffusion rate of the tip vortex produced by bursting is inevitable and will affect the intensity of other potential interactions with blades. This is one type of rotor wake problem that is poorly understood and difficult to model.

(а)Ц)„ = 12° (b) ^ = 23° Figure 10.14 A series of shadowgraph flow visualization images showing perpendicu­lar В Vis over the front of the rotor disk in forward flight, (a) xj/ь = 12°. (b) fb = 23°. (c) xj/b = 29°. (d) іkb = 39°. Free-stream flow is from left to right. Source: University of Maryland.