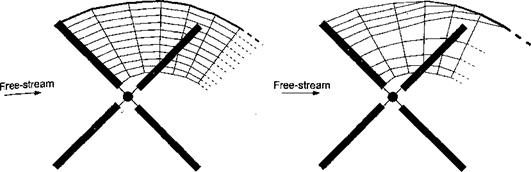
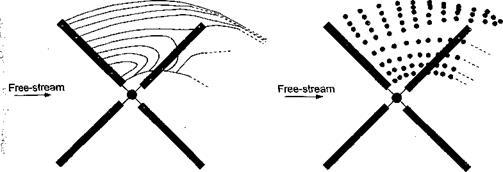
Vortex Models of the Rotor Wake

In vortex wake models, the convection of the tip vortices (and other concentrated vorticity) is explicitly tracked through the flow field relative to the rotor. Vortex diffusion and convection are, however, treated as separate steps. The underlying principle is that of Helmholtz’s law [see Lamb (1932) or Saffman (1992)], which embodies the principle of vorticity transport. Typically, the vortical wake is modeled by vortex lines[40] that are dis­cretized into the form of a regular lattice with straight elements [see Clark & Leiper (1970), Sadler (1971a, b), and Scully (1975)] or continuous curved vortex lines [see Quackenbush et al. (1988) and Wachspress et al. (2003)] or vortex “blobs” [see Lee & Na (1995, 1998)]. Schematics of these representations are shown in Fig. 10.26, where the wake from only one blade is shown for clarity. For most applications, the vortex wake model will be coupled to either a lifting-line or lifting-surface representation of the rotor blades (see Section 14.9). This defines the initial strengths and locations of the wake vortices relative to the rotor and forms boundary conditions for the remainder of the “far” vortex wake.

The main advantage of vortex methods, whether the approach be comprised of straight line vortex filaments, curved filaments, or vortex blobs, is that once the positions and strengths of the wake vorticity are obtained, then the induced velocity field at the rotor (or elsewhere, as required) can be computed by the use of the Biot-Savart law, followed by numerical integration over all of the filaments. The process lends itself readily to the computer. However, the main disadvantage of vortex methods is one of relatively high computational expense because many vortex elements are required to represent the wake of a helicopter rotor. While the evaluation of the Biot-Savart integral is trivial for a single vortex element, it is the very large number of elements required to model the entire rotor wake that determines the expense because a typical vortex filament may be discretized into several hundred or thousands of individual segments. For some applications in rotor analyses, it is the relatively high cost of vortex methods that limits their routine use. These methods are, however, still many orders of magnitude less expensive than finite-difference solutions based on the Euler or Navier-Stokes equations; see McCroskey (1995) and Section 14.2.1.

The principal differences among all of the various discretized vortex wake models that have been developed for helicopter applications are the assumptions and methods employed for the solution of the equations used to describe the transport of the wake vorticity. In prescribed vortex-wake models, the difficulties inherent in trying to explicitly solve these equations directly are avoided by either specifying the locations of the wake filaments a prion or by assuming an approximate velocity field near the rotor. Usually with the latter method, a simple velocity field (such as uniform or linear) can be prescribed that allows an analytical solution for the wake geometry. Alternatively, when specifying the wake geometry directly,

approximate functional relations can be derived from a combination of momentum theory and flow visualization experiments. In so-called “free” vortex wake methods, the solution for the wake is obtained from first principles. This form of solution recognizes that because parts of the vortices in the wake may interact with themselves (a self-induced effect) or with other vortices (a mutually induced effect) or with the blades themselves (BVI) the overall behavior of the wake cannot easily be generalized or prescribed in functional form and a numerical solutions must be sought. The development of numerical methods for this problem is considered in Section 10.7.6.