Modifications to Rigid Vortex Wake Models

Any number of assumptions about the induced velocity field near the rotor can be made to specify the right-hand side of Eq. 10.53 and decouple the equations. Other types of prescribed wake models for use in forward flight have also been derived on the basis of experimental observations. The advantage of these models is that, for some small additional computational effort, much better estimates of the rotor wake geometry can be obtained compared to a rigid wake. It has been observed from flow visualization experi­ments that the longitudinal and lateral distortions of the wake are relatively small compared to the vertical distortions. This means that the self-induced velocities in a plane parallel to the rotor plane are small: so for all the prescribed wake models it is still justified to use the undistorted tip vortex equations given previously by Eqs. 10.75 and 10.76. The differ­ences in the various prescribed wake models lie in the prescription of the vertical (axial) displacements of the tip vortices. Generally, these are defined using Eq. 10.77 as a basis, but with empirical or semi-empirical weighting functions being used to produce the wake distortions.

UTRC Generalized Wake Model

One such prescribed wake approach, used by Egolf & Landgrebe (1983), is called the Generalized Wake Model. The vertical displacements of the tip vortices are written as

(10.80)

right-hand side of the preceding equation is simply a modification to the undistorted rigid wake; the E term is called an envelope function and is effectively an amplitude term, and

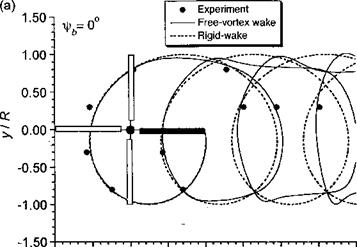
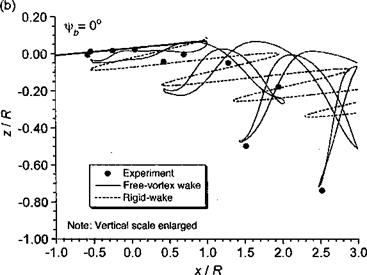
Figure 10.33 Representative rigid wake geometry in forward flight compared to free – vortex wake method and measurements, (a) Plan (top) view, (b) Side view, looking from retreating side. Four-bladed rotor; Cj = 0.008; fx — 0.15; a, = —3°. (Notice: Results for a four-bladed rotor have been computed, with the results for one blade being shown for clarity.)

the G term is a shape or geometric function. The vertical displacement envelope function is defined by

_ I fw exp(Ai for < 4л-,

I Mj/W + В for fw > 4n,

where the coefficients Ao, A, M, and В are functions of the number of blades, the ad­vance ratio, and the rotor thrust for a given rotor. The corresponding shape function
is given by the equations

N

E<« ‘nc cos n(fw – }fb) + g’ns sin n{fw – fh)} for 0 < < 2ж,

n= 0 N

Dc cos n(J/w – fh) + sin п(^ш – Vt?)} for tAu, > 2n,

n—0

where the coefficients g^c, g^s, g"c, and are functions of the number of blades and advance ratio for a given rotor. Usually N takes a value of 12.

Like the hover prescribed wake models, the coefficients of the forward flight model have been deduced from experimental studies of the wake geometry. However, because forward flight experiments are much more difficult and time consuming to undertake, there are less data available. Nevertheless, as shown by Egolf & Landgrebe (1983), the agreement of this prescribed wake model with measured wake geometries has been found to be good. As a consequence, there is usually a significant improvement in the prediction of blade airloads compared to those obtained using an undistorted rigid wake.