Free – Vortex Wake Analyses

General Concepts

Free-vortex wake models solve for the vortex strengths and rotor wake geometry, and in principle they do not require experimental results for formulation purposes, apart from the various assumptions that must be made. The position vectors of the individual wake filaments are now part of the solution process. Starting from some initial condition, which may be an undistorted rigid wake or a prescribed wake, the right-hand side of the equations must be computed through the repeated application of the Biot-Savart law with a desingularized core, which will likely include a core growth (vorticity diffusion) model. The solution for the wake geometry then proceeds until convergence, which usually means that a periodic solution is obtained. Pioneering work on the FVM applied to rotor wakes was performed by Landgrebe (1969, 1971, 1972), Clark & Leiper (1970), Sadler (197la, b), and Scully (1975), and many variations and developments of the FVM have subsequently followed. The results obtained with the FVM are probably qualitatively correct no matter what type of numerical scheme and vortex model are used. However, the quantitative pre­dictions made using these methods are much less absolute, and their true capabilities can only be determined though careful and systematic correlation studies with experimental measurements.

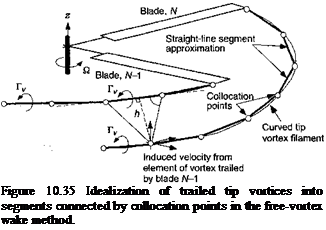
In the first instance, consider the rolled up tip vortices generated by each blade. For a rotor with Nb blades there will be an equal number of intertwining tip vortices (see Fig. 10.35). Generally, the filaments will have unequal circulation strengths along their length, which can be related to the lift (circulation) on the blade at the time of their formation. This means that both trailed and shed elements must be included in the solution to satisfy conservation of circulation. However, because this increases dramatically the number of free elements and the numerical costs, a tip vortex of average strength related to the rotor thrust (blade loading) is often assumed (see Section 3.3.8). A series of collocation points can be specified on the trailed vortex filaments, and these points are numerically convected through the flow field at the local velocity in accordance with the transport equation defined previously in Eq. 10.53.

General Solution Methodologies

Free-vortex wake models can be divided into two general types of solution method­ologies: 1. Time-stepping or time-marching methods, and 2. Relaxation or iterative meth­ods – see Leishman et al. (2002b). In the time-stepping method, the solution can be developed by an impulsive start of the rotor with no initial wake. The boundary condition specifies that each trailed vortex filament be attached to the blade at its point of origin, = 0. Alternatively, a prescribed wake geometry can be specified as an initial condition. In either case, the solution is stepped in the ^ (azimuthal) direction using a time integration scheme, and for a steady-state flight condition, a converged solution is obtained when the transients introduced by the initial condition die out and a periodic solution is achieved. The relaxation method, in contrast, specifies that the trailed vortex elements be attached to the blades as an initial condition, whereas periodicity is enforced as the boundary condition. The solution is stepped in the direction in an iterative manner, and convergence is obtained once the wake vortex geometry no longer distorts between successive iterations. Relaxation schemes have the advantage that they are numerically more efficient because periodicity of the wake solution can be imposed as a boundary condition. Also, relaxation schemes are generally free of the numerical instabilities that are often produced in some time-marching schemes as a consequence of round-off errors.

Different numerical schemes can also be used within both the time-stepping and relax­ation approaches (i. e., explicit, implicit, or hybrid). Several rotor wake analyses use explicit type methods, which are simple in concept, but are particularly prone to various numerical problems associated with round-off errors. Consider, as an example, a representative PDE describing the convection of the vortex filaments such as

Spatial discretization would result in reducing this partial differential equation into a system of simultaneous ODEs that can be written as

dr

— = Ar + ПГ).

where A is the space discretization matrix. An explicit method for this equation would use a finite-difference scheme such as

(10.89)

Notice that the updated value of r at time n + 1 is based on values from the previous time step alone. Although this is one of the simplest methods, the truncation error in the solution for r is of order (At)2 per time step, and so the error can grow rapidly if the time step is too large. The high computational costs of most blade element based rotor analyses often require relatively large time (blade azimuth or Афь) steps with the wake solution, making the assessment of truncation errors an important consideration..

Implicit methods, in contrast, are free from many of these numerical problems. An implicit difference scheme to solve the example equation in Eq. 10.87 is

rn+ _ rn-+ At [Arn+І + v(r«+i)j _ (10.90)

In this case, the right-hand side also requires the evaluation of terms at the (n – j – l)th step, information that has not yet been determined. If the velocity term, V, is a simple function of r, then the equation can be easily simplified and solved as a set of simultaneous equations. For more complex velocity functions, however, V must first be linearized using a Taylor expansion, resulting in a semi-implicit scheme. This approach was applied to the FVM by Miller & Bliss (1993). While numerical errors are much smaller with this intensive computer-processing technique, it is not routinely used because it requires the simultaneous solution of a large set of linear equations at each time step.

A multistep or predictor-corrector method may also be used to solve the wake equations. In this approach, an explicit method is used to generate an approximate value for the current step

rn+l = rn + At [Arn + V(rn)], (10.91)

and this approximate, or predicted value, r, is then used to generate the final approximation to r"+1 using a corrector step such as

rn+l = rn + At [Arn+i + V'(rn+1)] . (10.92)

Predictor-corrector methods have a truncation error per step of order (At)3 and exhibit considerably better stability characteristics than explicit methods alone – see Crouse & Leishman (1993). They also require much less computation than implicit or semi-implicit schemes. However, this scheme requires two velocity field calculations per time step com­pared to one for an explicit method (see Question 10.8).

Bagai & Leishman (1995a, b; 1996) have further developed a FVM for rotor wake modeling based on a predictor-corrector scheme in a relaxation formulation, but with two modifications. First, the explicit predictor step is modified into the pseudo-implicit equation

~n+i =rn + At [дрп-и + . (10.93)

While the forcing (velocity) function is calculated explicitly from the previous time step, the position vectors at the current time-step also appear on the right-hand side (P+1). The above predictor equation, therefore, is no longer fully explicit. Second, the corrector step incorporates an averaging scheme whereby an average of the velocity function from the previous time step and the predicted value are used to update the corrected position vectors. This helps to improve the stability characteristics of the scheme. Once again, the position vectors at the current time step also appear on the right-hand side, also making the corrector step a pseudo-implicit equation, that is