Wake Stability Analysis

The tendency of a helicopter rotor wake toward developing an instability is an in­herent characteristic because of the naturally unstable deformation modes associated with its helicoidal form. Various aerodynamic disturbances inherent in nature, or physical dis­turbances associated with the manner in which the rotor is operated, usually provide the conditions necessary to excite the equilibrium wake geometry and cause it to exhibit per­turbations. This problem has been examined theoretically by Levy & Forsdyke (1928), Widnall (1972), Gupta & Lowey (1974), and Bhagwat & Leishman (2000b). In particular, a local long-wave wake perturbation known as vortex “pairing,” has already been mentioned in Section 10.5.2. This is a combined low-frequency/long-wavelength radial and axial de­formation mode and has been observed in several rotor wake experiments, for example, Tangier et al. (1973), Martin et al. (1999), and Caradonna et al. (1999).

While wake instabilities seem common enough in experiments documenting rotor wakes, in computational modeling it is the omnipresent numerical truncation and round-off errors that potentially initiate wake instabilities. Properly distinguishing between the consequences

of physical and numerical wake instabilities has been a long-standing problem in helicopter aerodynamics. This problem was examined by Bhagwat & Leishman (2000b) using vortex theory and also by Martin et al. (1999) in rotor experiments designed to deliberately pro­mote wake instabilities. A two-bladed rotor wake was shown to develop a primary mode of instability with a wave number at the rotational frequency of the rotor. This mode it seems, is relatively easy to excite in a real rotor flow field, such as by blade mistracking. The argu­ment can be carried forth to rotors with greater numbers of blades, where the susceptibility to develop wake instabilities always increases with blade number. This fundamental char­acteristic behavior of rotor wakes is key to how various forms of physical wake instabilities actually arise in practice.

The stability of a rotor wake can be examined mathematically from a perturbation analy­sis. From the equilibrium solution for the wake, such as by using vortex theory, the solution is then perturbed by a small quantity, Sr, with the new geometry being described by r + Sr. The governing equation for this perturbed wake geometry is given by

The equation governing the perturbation wake displacement, Sr, is obtained by subtracting the equilibrium equation from the perturbed equation (Eq. 10.102) giving

d{8r)

= V(r + Sr) – V(r). (10.103)

dt

The induced velocity on the RHS of Eq. 10.102 can be expressed as a Taylor series in Sr as

This can now be linearized by neglecting higher-order terms in Sr to give

which is the equation governing the perturbation problem.

For the solution of Eq. 10.105, perturbations to the wake can be assumed to be in the form of a normal mode (or a traveling wave) along the lengths of the vortex filaments – see Saffman (1992) and Bhagwat & Leishman (2000b). Because of the helicoidal nature of the rotor wakes, cylindrical polar coordinates can be used. In this case the normal mode perturbation is given by

where or is the growth rate and to is the wave number, that is the perturbation wave has со cycles for each rotor revolution. The governing equations for each perturbation mode can then be solved at a given point P on the vortex filament. The velocity contributions of all the vortex elements are summed using the Biot-Savart law to obtain the total induced velocity perturbation in matrix form as [F] = [u,]. After some manipulation, the problem can

І

be reduced to a standard eigenvalue problem with the form

otp{x} = [M]P {*},

where M is the fundamental solution matrix for the wake, the evaluation of which is completely described by Bhagwat & Leishman (2000b). The eigenvalues aP give the growth

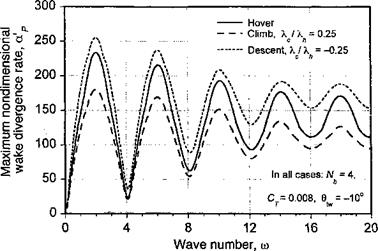
Figure 10.43 Maximum nondimensional wake divergence rates as a function of wave number со for a four-bladed rotor in axial flight (hover, climb, and descent).

rate of the perturbation at a point P on the vortex wake. A positive growth corresponds to an unstable wake mode, a zero growth rate is a neutrally stable wake mode, and a negative growth rate is a stable wake mode.

The advantage of this type of mathematical approach is that the fundamental stability of the rotor wake can be understood in terms of its characteristics (shape and circulation strengths) and, therefore, how the stability of the wake is affected by the various geometric and operational characteristics of the rotor. For example, climbing or descending flight changes significantly the helicoidal pitch of the rotor wake structure, and so this must affect the overall wake stability. The rotor thrust (disk loading) and blade twist are also known to be factors that affect the stability of the rotor wake.

Figure 10.43 shows an example of the stability characteristics of a rotor wake in axial flight. The wave numbers corresponding to the extrema in the wake divergence rates correlate with the number of interdigitated tip vortex filaments (or blades). On one hand, the maximum divergence rate occurs at wave numbers equal to half-integer multiples of the number of blades, that is, at wave numbers со = (к + 1/2)Nb for all integer k. On the other hand, a minimum divergence rate occurs at integer multiple of the number of blades, that is for со = к Nb. With increasing wave number, the difference between maximum and minimum divergence rates decreases, indicating that for very large wave numbers the divergence rates would be independent of wave number. However, the increasing growth rates for large wave numbers with increasing number of filaments suggests an increased overall susceptibility to wake instabilities, say those that might be produced by random disturbances or turbulence in the flow.

‘rhis figure also shows that a climb velocity decreases the wake growth rates (i. e., the wake is less susceptible to instability and to forming wake perturbations). This is because of the increased helicoidal spacing between adjacent wake filaments. The results in Fig. 10.43 also show that for the descending rotor a more substantial increase in growth rates are obtained for wake modes at the higher wave numbers. This implies an increased suscep­tibility to instability and to forming wake perturbations in descending flight. These might be triggered by the higher-frequency unsteady airloads generated at the rotor, or by atmo­spheric turbulence, rather than by larger-scale disturbances in the surrounding flow. This
observation may be key to the full understanding of the initiation mechanisms of wake instabilities. However, it may also prove to be an impediment to the achievement of reliable numerical predictions for rotor wakes under various descending flight conditions because of the need to model the source of these disturbances.