Blade Element Model for the Wind Turbine

The aerodynamic analysis of the wind turbine can be approached readily from the perspective of the blade element model, which has been discussed previously in Chapter 3 for the helicopter. In this case, the flow model is similar to the helicopter rotor in a descending flight condition (discussed in Section 2.13.2), with the flow upward toward the plane of the

 

(a) Front view

Qy

R

У

▲

z®———— ►x

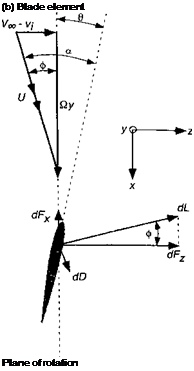
Figure 13.9 Blade element model for a wind turbine operating in axial (unyawed) flow.

rotating blades, as shown in Fig. 13.9. The local pitch angle of the blade element is в so that the AoA at the blade element[47] is a = в + ф. The inflow modifies the direction of the relative flow velocity vector and, therefore, alters the AoA at each blade element from its 2-D value. It will be apparent that it is the forward inclination of the lift vector that provides a component of force to overcome the drag (profile and induced) on each element and so produces the net in-plane force that will drive the turbine and produce power at the shaft. This is analogous to the autorotational condition for the helicopter.

Assume that the swirl component in the flow near the turbine and its wake is small and can be neglected. The resultant incremental lift dL and drag dD per unit span on the blade element are

1 9 1 „ ___________________________________________________

dL = – pU cCi dy and dD = – pU*cCd dy, (13.26)

where Ci and Cd are the lift and drag coefficients, respectively, and the resultant flow velocity U ^ Qy. Wake swirl may be included into U, however, based on a knowledge of the helicopter flow field, swirl is small at lower thrust coefficients and/or higher tip speed ratios (see page 69). The lift dL and drag dD act perpendicular and parallel to the resultant flow velocity, respectively. Notice that the quantity c is the local blade chord. From Fig. 13.9

it is apparent that these forces can be resolved perpendicular and parallel to the rotor disk plane giving

dFz = dL cos ф + dDsiiup and dFx = dL sin0 — dDcoscp. (13.27)

The contributions to the thrust, torque, and power of the rotor are thus

dT = Nb dFz, dQ = Nby dFx and dP = NbQy dFx, (13.28)

where Nb is the number of blades comprising the turbine rotor. This also assumes no precone on the blades, which can be significant for wind turbines. Such effects can be approximately incorporated by multiplying dCT by cos fP, where f>p is the precone angle. Furthermore, notice that unless the turbine is yawed with respect to the wind, the aerodynamic environment is (ideally) axisymmetric, and the airloads are independent of the blade azimuth angle and that there is no wind shear. Substituting the results for dFx and dFz from Eq. 13.27 gives

dT = Nb(dL cos ф + dD sirup), (13.29)

dQ = Nb{dL sixuf) — dD cos ф)у, (13.30)

dP = Nb(dL sin0 — dDcos(f>)Qy. (13.31)

Applying small angle simplifications to the preceding equations (see page 118) gives

dT = Nb{dL + <f>dD), (13.32)

dQ = Nb(4>dL – dD)y, (13.33)

dP = NbQ((f>dL – dD)y. (13.34)

me incremental thrust coefficient on the turbine then

_ NbdL _ Nb(jp(Qy)2c(Ci +.pCd) dy)

T ~ {pAVl ~ p^R2)V^

= (Q + фСа) dr = oX2(Q + фСа) dr,

where r = у/R,(7 = Nbc/irR is the local or chord solidity of the rotor and X — Qy/Voo is the local section speed ratio. It will be apparent that the local section speed ratio can be written as

у _ Qy _ QR Ґ Qy _ _

Voo Voo S2R)

Therefore, the incremental thrust coefficient becomes simply

ИГг = гтУ2 (Г. 4- ЛГ Лг2 Иг

——- ± TSRV“‘ ‘ ^———————–

Proceeding in a similar manner to find the incremental power coefficient dCp leads to

dCp = о(фСі — Cd)r3 dr.

It will also be apparent that the inflow angle can be written as

(13.40)

The fundamental equations for the analysis of the wind turbine by means of the blade element theory have now been established. However, to evaluate Cp and Cp it is necessary to predict the spanwise variation in the induced inflow u, (or the induction ratio a) as well as the sectional aerodynamic force coefficients, Q and Cd – Also, a = «(Voo, 0, u,), and Vi = vfr). As for the helicopter, clearly a fundamental problem for the wind turbine is to determine the induced velocity Vi (or a), which has its origin for the most part in the physics of the downstream wake. This aside for now, if 2-D aerodynamics are assumed, then Q = Ci(a, Re)mdCd = Q(a, Re), where Re is the local Reynolds number.[48] See Tangier (2002) and Coton et al. (2002) for a discussion of how 2-D airfoil measurements can he integrated into the blade element approach and the various practical problems associated with this. Because these airfoil section characteristics cannot, in general, be expressed as simple analytic results it is usually necessary to use table look-up approaches (Section 7.11.3) and to solve the integrals for CT and Cp by numerical integration. However, it is possible to proceed further by assuming linear aerodynamics and by invoking the principles of the blade element momentum theory. This has been discussed in Section 3.3 for the helicopter.