Variation of Induced Velocity with Axial Distance

In subsequent material the variation of the induced velocity with axial distance from the propeller disk plane is needed. This variation can be

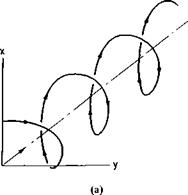
Fig. 4-13. Geometry of a helical vortex.

found approximately by calculating the axial velocity induced along the axis of a semi-infinite helical vortex filament by using the Biot-Savart law. A vortex helix is shown in Fig. 4-13a and a segment of the helix in Fig. 4-13fi.

If p is the pitch of the helix, the equation of the helix in terms of the generating angle 0 is

x = R cos 0,

у — R sin

7 = P± 2n

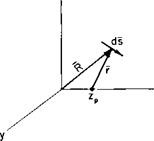
If R is the radius vector from the origin to a differential element of the vortex, then for a point zp along the z-axis the radius vector r from zp to a differential element ds is

r = R – kzp

or

r = іR cos 0 + jR sin 0 +

The differential element of the vortex is simply dR, where

R = iR cos 0 + R sin 0 + к

so that

ds = ( — iR sin 0 + jR cos 0 + 1 ) dO.

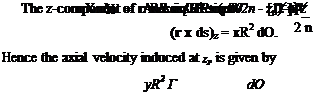Thus

This integrates to

Finally in terms of the velocity induced at the propeller disk (zp = 0), the axially induced velocity becomes

wa(0) Уі + (z/R)2

Observe that for (z/R) = — oo, (4-54) is equal to zero, whereas for (z/R) = + oo the velocity ratio is equal to 2 in agreement with the results of momentum theory.

Static Performance

In almost any paper on the design analyses of VTOL aircraft in which different configurations are compared a graph reflecting the static perform-

ance of propellers can be found. This graph usually takes the form of static thrust capability (lb/hp) versus disk loading (lb/sq ft). Not to be outdone, this book includes such a graph (see Fig. 4-14), which was prepared in the following manner.

First, from experience it is known that the induced power is approximately 15% higher than that predicted by momentum theory. Second, it is assumed

that the chord and Cd are independent of radius and that a, is small so that VR ~ cor. Hence, approximately,

550 hp = 1.15 + BPcC^mR)3R s/2 pA 8

(4-55)

By rewriting Cd in terms of the lift-drag ratio є and an average C, and dividing by T we obtain

hp = 1.15 s/TjA BCpeCL(ooR)3R T 550 s/^F (8)550Г

but

L Bpcco2R3 Be a ——— nR

and

Hence

hp _ U5 JtJa 3coRe T 550 ^2F 4(550)

(4-56)

and

(4.57) A 6 Figure 4-14 was prepared for standard sea-level conditions for an average CL of 0.5 and a tip speed of 800 fps. The solidity required to maintain these conditions is also illustrated. An e of 0.03 was assumed for the calculations. Also shown in the figure are the ranges in which various types of aircraft normally operate. Further considerations on the static performance of helicopter rotors are undertaken in Chapter 5.

Problems 1. An aircraft has an equivalent flat-plate area of 2 sq ft, an elliptic wing of aspect ratio 6 with an area of 160 sq ft, and a gross weight of 2000 lb. Its engine develops 150 shaft horsepower at 2500 rpm. At SSL conditions,

and equipped with a 6 ft-diameter propeller with the characteristics of Fig. 4-11, what will be its maximum speed?

2. What would Fmax be for the aircraft of Problem 1 equipped with an ideal propeller with no profile drag?

3. Given the propeller in Fig. 4-12, estimate the section C, for a J of 1.0 at r = 3R/4. Note that /1 is the pitch angle of the chord line.

4. Estimate the initial acceleration of the aircraft in Problem 1 on takeoff.

5. A 10-bladed special-purpose propeller has a constant 10-in. chord and a 12% thick airfoil section and is designed to operate at an advance ratio of 1.5. Calculate the correction to the section angle of attack at a radius of 20 in. The propeller has a diameter of 6 ft.