Bernoulli’s Equation

Bernoulli’s equation is well known in fluid mechanics and relates the pressure to the velocity along a streamline in an inviscid, incompressible flow. It was first formulated by Euler in the middle 1700s. The derivation of this equation follows from Euler’s equations using the fact that along a streamline the velocity vector is tangential to the streamline.

dx _ dy dz

U V w

First, multiply Equation 2.22a through by dx and then substitute Equation 2.26 for v dx and w dx. Also, the first term of the equation will be set equal to zero; that is, at this time only steady flow will be considered.

Similarly, multiply Equation 2.22b by dy, Equation 2.22c by dz, and substitute Equation 2.26 for и dy, w dy and и dz, v dz, respectively. Adding the three equations results in perfect differentials for p and V2, V being the magnitude of the resultant velocity along the streamline. This last term results from the fact that

du 1 du2

dx 2 dx

and

V2 = u2 + v2+ w

Thus, along a streamline, Euler’s equations become

V dV + —= 0

If p is not a function of p (i. e., the flow is incompressible), Equation 2.27 can be integrated immediately to give

P + 2pV2 = constant (2.28)

If the flow is uniform at infinity, Equation 2.28 becomes

P + 2pV2 = constant = p« + 2PVJ (2.29)

Here V is the magnitude of the local velocity and p is the local static pressure. V. and p„ are the corresponding free-stream values. Equation 2.29 is known as Bernoulli’s equation.

The counterpart to Equation 2.29 for compressible flow is obtained by assuming pressure and density changes to follow an isentropic process. For such a process,

plpy = constant (2.30)

у is the ratio of the specific heat at constant pressure to the specific heat at constant volume and is equal approximately to 1.4 for air. Substituting Equation 2,30 into Equation 2.27 and integrating leads to an equation some­times referred to as the compressible Bernoulli’s equation.

Xr H—2_ — = constant (2.31)

2 у 1 p

This equation can be written in terms of the acoustic velocity. First it is necessary to derive the acoustic velocity, which can be done by the use of the momentum theorem and continuity. Figure 2.9 assumes the possibility of a stationary disturbance in a steady flow across which the pressure, density, and velocity change by small increments. In the absence of body forces and viscosity, the momentum theorem gives

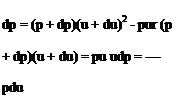But, from continuity, or

Thus

и + du ————

P + dp, p + dp

Figure 2.9 A stationary small disturbance in a steady compressible flow.

If the small disturbance is stationary in the steady flow having a velocity of u, then obviously и is the velocity of the disturbance relative to the fluid. By definition,- it follows that u, given by Equation 2.32, is the acoustic velocity. By the use of Equation 2.30, the acoustic velocity is obtained as

(2.33)

An alternate form, using the equation of state (Equation 2.1), is

a = (yRT)m (2.34)

Thus Equation 2.31 can be written

V2 a2

~2 + = constant (2.35)

The acoustic velocity is also included in Figure 2.3 for the standard atmos­phere.

Determination of Free-Stream Velocity

At low speeds (compared to the acoustic velocity) a gas flow is essen­tially incompressible. In this case, and for that of a liquid, Equation 2.29 applies. If the fluid is brought to rest so that the local velocity is zero then, from Equation 2.29, the local pressure, referred to in this case as the stagnation or total pressure, is equal to> the sum of the free-stream static pressure, p„, and pVj/2. This latter term is called the dynamic pressure and is frequently denoted by the symbol q. Thus,

-P P

where p0 is the total pressure, also referred to as the stagnation or reservoir pressure. The pitot-static tube shown in Figure 2.2 measures (po — p«) and is probably the most common means used to determine airspeed. However, notice that Equation 2.36 contains the mass density that must be determined before the airspeed can be calculated. This is most readily achieved by measuring, in addition to the difference between the stagnation pressure and the static pressure, the static pressure itself and the temperature. The density is then determined from the equation of state (Equation 2.1).

At higher speeds (and we will now examine what is high) Equation 2.29 no longer holds, so that V» must be determined from Equation 2.31.

V2 , 7 P _ 7 Po

2 у – 1 p у – 1 p0

At this point the subscript °° has been dropped, so that p, p, and V without a subscript may be local or free-stream values.

Remembering that yplp is the square of the acoustic velocity, the preceding equation becomes

M2 | 1 _ 1 pop

2 у – 1 у – 1 p po

Using Equation 2.30, this can be written as

The dynamic pressure, q, is defined as

q = PV2 (2.38)

which can be written in terms of the Mach number as

q = |урЛ#

Combining this with Equation 2.37 gives

The square root of Equation 2.39 is presented graphically in Figure 2.10. The departure of this function from unity is a measure of the error to be incurred in calculating the airspeed from the incompressible Bernoulli equa­tion. Below a Mach number of 0.5 the error is seen to be less than 3%.