Chord of an Aerofoil

For a cylindrical aerofoil (that is, a wing for which the profiles are the same at every location along the span, as shown in Figure 1.5), the chord of the aerofoil is taken to be the chord of the profile in which the plane of symmetry cuts the aerofoil. In all other cases, the chord of the aerofoil is defined as the mean or average chord located in the plane of symmetry.

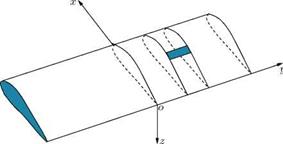
Let us consider a wing with rectangular Cartesian coordinate axes, as shown in Figure 1.10. The x-axis, or longitudinal axis, is in the direction of motion, and is in the plane of symmetry; the y-axis, or lateral

axis, is normal to the plane of symmetry and along the (straight) trailing edge. The z-axis, or normal axis, is perpendicular to the other two axes in the sense that the three axes form a right-handed system. This means, in particular, that in a straight horizontal flight the z-axis will be directed vertically downwards. Consider a profile whose distance from the plane of symmetry is |y|. Let c be the chord length of this profile, в be the inclination of the chord to the xy plane, and (x, y, z) be the coordinates of the quarter point of the chord, that is, the point of the chord at a distance c/4 from the leading edge of the profile. This point is usually referred to as the quarter chord point. Since the profile is completely defined when y is given, all quantities characterizing the profile, namely, the mean chord, its position and inclination to the flow, are functions of y.

The chord of an aerofoil is defined by averaging the distance between the leading and trailing edges of the profiles at different locations along the span. Thus, if cm is the length of the mean chord, (xm, 0, zm) its quarter point, and вт its inclination, we take the

These mean values completely define the chord of the aerofoil in length (cm), direction (em), and position

(xm, zm).