Helmholtz’s Theorems

The four fundamental theorems governing vortex motion in an inviscid flow are called Helmholtz’s theorems (named after the author of these theorems). The first theorem refers to a fluid particle (or element) in general motion possessing all or some of the following:

• Linear velocity.

• Vorticity.

• Distortion.

This theorem has been discussed in part in Section 5.3, where the vorticity was explained and its expression in Cartesian or polar coordinates were derived. Helmholtz’s first theorem states that:

“the circulation of a vortex tube is constant at all cross-sections along the tube."

The second theorem demonstrates that:

“the strength of a vortex tube (that is, the circulation) is constant along its length."

This is sometimes referred to as the equation of vortex continuity. It can be shown that the strength of a vortex cannot grow or diminish along its axis or length. The strength of a vortex is the magnitude of the circulation around it, and is equal to the product of vorticity Z and area S. Thus:

Г = ZS.

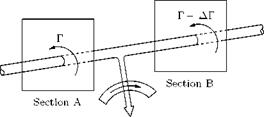
It follows from the second theorem that, Z S is constant along the vortex tube (or filament), so that if the cross-sectional area diminishes, the vorticity increases and vice versa. Since infinite vorticity is unacceptable, the cross-sectional area S cannot diminish to zero. In other words, a vortex cannot end in the fluid. In reality the vortex must form a closed loop, or originate (or terminate) in a discontinuity in the fluid such as a solid body or a surface of separation. In a different form it may be stated that a vortex tube cannot change its strength between two sections unless vortex filaments of equivalent strength join or leave the vortex tube, as shown in Figure 5.11.

It is seen that at section A the vortex tube strength is Г. Downstream of section A an opposite vortex filament of strength —АГ joins the vortex tube. Therefore, at section B, the strength of the vortex tube is:

Г = Г – АГ

as shown in Figure 5.11. This is of great importance to the vortex theory of lift.

The third theorem demonstrates that a vortex tube consists of the same particles of fluid, that is: “there is no fluid interchange between the vortex tube and surrounding fluid."

The fourth theorem states that:

“the strength of a vortex remains constant in time."