Calculation of uR, the Velocity due to Rotational Flow

We see that Equation (5.24) is satisfied if uR is represented as the curl of a new, yet unknown, vector field a. Thus:

 

(5.28)

 

uR = curl a = v x a.

 

We know that the divergence of the curl always vanishes.3 Therefore:

 

V • (v x a) = v • ur = 0.

 

(5.29)

 

Now let us form the curl of u and, from Equation (5.23), obtain the equation:

 

v x (u) — v x (v x a) .

 

(5.30)

 

But using the vector identity:

 

txu — v (v • u) v x (v x u) .

 

3Indeed, this is true for any vector, for example, if a and b are vectors, a • (a x b) = [aab] = 0. Therefore, in general, it can be expressed, [v v a] = 0, where v and a are vectors. The representation “[ ]” is termed “box” notation in vector algebra.

 

We can express Equation (5.30) as:

v x u = v (V • a) — Aa. (5.31)

Up to now the only condition on vector a is to satisfy Equation (5.28). But this condition does not uniquely determine this vector, because we can always add the gradient of some other function f to a without changing Equation (5.28), since v x v f = 0. If, in addition, we want the divergence of a to vanish (that is, v • a = 0), we obtain from Equation (5.31) the simpler equation:

V x u = — Aa. (5.32)

In this equation, let us consider v x u as a given vector function b(x), which is determined by the choice of the vector filament and its strength (that is, circulation). Thus, the Cartesian component form of the vector Equation (5.32) leads to three Poisson’s equations, namely:

Aa; = — b;; i = 1, 2, 3. (5.33)

For each of these component equations, we can apply the solution [Equation (5.27)] of Poisson’s equation. Now, vectorially combining the result, we can write the solution for a, from Equation (5.32), in short as:

Thus, calculation of the velocity field u(x) for a given distribution g(x) = div u and b(x) = curl u is reduced to the following integration processes, which may have to be done numerically:

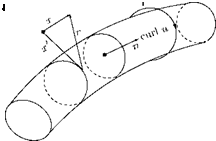
Now, let us calculate the solenoidal term of the velocity uR, using Equation (5.35). This is the only term in incompressible flow without internal boundaries. Consider a field which is irrotational outside the vortex filament, shown in Figure 5.20.

The velocity field outside the filament is given by: