Quadruplication of the Integral Equation for a Wing of Finite Span

The above approach can be extended to the case of an arbitrary aspect ratio Л h. The relevant integral equation can be written in the form

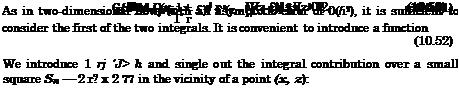where ys = ya(x, z),

where xe = xe(z) is the equation of the leading edge. We turn to considera­tion of the following integral

Now, we turn to the integral

=

it is easy to find the lowest order representation of I12:

Summing up expressions (10.59) and (10.62), we find that the limiting asymp­totic form of the integral equation for a wing of finite aspect ratio is identical to the Poisson differential equation

Equation (10.63) has to be solved in the interior of the two-dimensional do­main 5, bounded by the wing’s planform contour. The boundary conditions for (10.63) can be either derived by the matching procedure or adopted on the basis of appropriate physical requirements (e. g., continuity of the circu­lation at the leading and side edges and continuity of the pressure at the trailing edge). As expected, equation (10.63) is identical to that obtained earlier within the boundary problem formulation; see formula (3.59).