Characteristic Helicopter Horizontal Flight Spe

The characteristic horizontal flight speeds define to a considerable degree the helicopter flight qualities. Calculation of these speeds, and then their verification in flight, is one of the important problems of helicopter aerodynamic design. The calculation of the characteristic speeds is most often made using the power method, first suggested by Zhukovskiy.

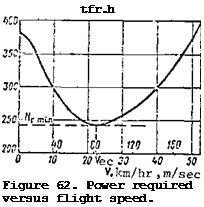
To construct the power required and available curves we use the curve of Figure 62. We find the power available at rated and takeoff engine rpm from the formulas

N.. = N I,
avail e

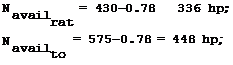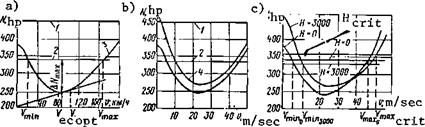
We use these values to plot a curve (Figure 63a), which permits deter­mining the following characteristic horizontal helicopter flight speeds:

Figure 63. Power required and available as a function of helicopter we ight and flight 1) N a for H = 0, n = 2200 rpm; 2) N a for H = 0, n – 2050 rpm; 3) Nh for H = 0, G = 2200 kgf; 4) Nh for H = 0, G = 2300 kgf.

1. The maximal speed, which corresponds to the point of intersection of the power required and available curves. When using rated engine power, the maximal horizontal flight speed at sea level will be about 165 km/hr; when using takeoff power, this speed will be 208 km/hr.

2. The optimal velocity at which the longest flight range is obtained.

This speed corresponds to the point of contact of a tangent drawn from the coordinate origin to the power required curve (for the Mi-1, V t = 90-95 km/hr),

3. The economical speed, i. e., the speed corresponding to minimal power required (for the Mi-1, Vgc = 80 km/hr).

4. The minimal speed. When using rated power at a flight weight of /94

2200 kgf, the helicopter cannot hover at sea level. It can only perform hori­zontal flight with a speed of about 20 km/hr. However, heavy vibration develops at low speed; therefore, the constructor has established speed limi­tations: minimal permissible is 40 km/hr, maximal permissible is 170 km/hr.

5. The horizontal flight speed range, i. e., the speeds at which horizon­tal flight is possible. When using rated power the speed range is

ду = V – V. = 165 – 20 = 145 km/hr.

rat max mxn

When using more than rated power, the total speed range is V t = 170 – 0 = = 170 km/hr.

6. The excess power, i. e., the difference between the power available and required for horizontal flight at a given speed. Each speed is associated with a given excess power AN = ^ – N^. The maximal excess power will

occur for flight at the economical speed.