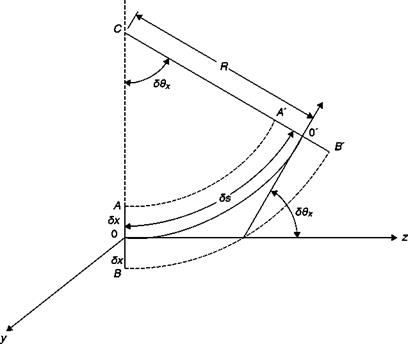
Deflection of a light beam in the presence of a constant gradient of refractive index

Assume that the beam, which initially propagates in the z direction, encounters a zone where there is a gradient of refractive index

Deviation of a light beam in the presence of a constant gradient of refractive index

x ■f

(Figure 6.15). Denoting with n the refractive index at the point 0, at points A and B of the beam, at a distance of ±8x from the z axis, the refractive index takes the values respectively:

Эл Эл. ,

nA = n+——ox nB = n – — ox (6.3)

dx dx

Since there is an inverse relationship between the refractive index and the speed of light, c, the speed of light at points A and B is such that:

dn s

л——- ox

dx dn „

n+— ox dx

therefore, the beam deflects toward the positive x axis. After a time, 8t the wave front AB is in the position A’B’ deflected by the angle 8Qx with

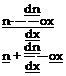respect to AB. The rays passing through A and B in time 8t travel distances SsA and 8sB proportional to the speeds cA and cB, respectively. Indicating with R the radius of curvature of the ray passing through the origin of the axes, we can write:

which yields:

which is the required relationship between the deflection of the light rays and the gradient of the index of refraction.

Similarly, if there is a gradient of n in the y direction, constant and greater than zero, the beam undergoes a deflection towards the positive y axis given by:

So, =1 ^Ss

n dy

The total deflections that the beam suffers through a test chamber of width L are therefore, respectively:

where s can be replaced with z as the deviations are usually infinitesimal.