FUNDAMENTALS OF LIFT THEORY

2- 2-1 Kutta-J oukowsky Lift Theorem

Treatment of the theory of lift of a body in a fluid flow is considerably less difficult than that of drag because the theory of drag requires incorporation of the viscosity of the fluid. The lift, however, can be obtained in very good approximation from the theory of in viscid flow. The following discussions may be based, therefore, on inviscid, incompressible flow.[5] For treatment of the problem of plane (two-dimensional) flow about an airfoil, it is assumed that the lift-producing body is a very long cylinder (theoretically of infinite length) that lies normal to the
flow direction. Then, all flow processes are equal in every cross section normal to the generatrix of the cylinder; that is, flow about an airfoil of infinite length is two-dimensional. The theory for the calculation of the lift of such an airfoil of infinite span is also termed profile theory (Chap. 2). Particular flow processes that have a marked effect on both lift and drag take place at the wing tips of finite-span wings. These processes are described by the theory of the wing of finite span (Chaps. 3 and 4).

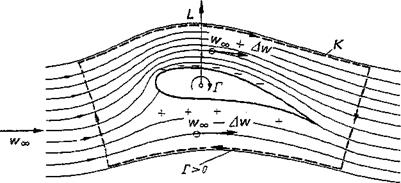
Lift production on an airfoil is closely related to the circulation of its velocity near-field. Let us explain this interrelationship qualitatively. The flow about an airfoil profile with lift is shown in Fig. 24. The lift L is the resultant of the pressure forces on the lower and upper surfaces of the contour. Relative to the pressure at large distance from tire profile, there is higher pressure on the lower surface, lower pressure on the upper surface. It follows, then, from the Bernoulli equation, that the velocities on the lower and upper surfaces are lower or higher, respectively, than the velocity w» of the incident flow. With these facts in mind, it is easily seen from Fig. 24 that the circulation, taken as the line integral of the velocity along the closed curve К, differs from zero. But also for a curve lying very close to the profile, the circulation is unequal to zero if lift is produced. The velocity field ambient to the profile can be thought to have been produced by a clockwise-turning vortex Г that is located in the airfoil. This vortex, which apparently is of basic importance for the creation of lift, is called the bound vortex of the wing.

In plane flow, the quantitative interrelation of lift L, incident flow velocity vv«,, and circulation Г is given by the Kutta-Joukowsky equation. Its simplified derivation, which will now be given, is not quite correct but has the virtue of being particularly plain. Let us cut out of the infinitely long airfoil a section of width b (Fig. 2-5), and of this a strip of depth dx parallel to the leading edge. This strip of planform area dA=bdx is subject to a lift dL = (рг—ри) dA because of the pressure difference between the lower and upper surfaces of the airfoil. The vector dL can be assumed to be normal to the direction of incident flow if the small angles are neglected that are formed between the surface elements and the incident flow direction.

The pressure difference between the lower and upper surfaces of the airfoil can be expressed through the velocities on the lower and upper surfaces by applying the

Figure 2-4 Flow around an airfoil profile with lift Z,. r = circulation of the airfoil.

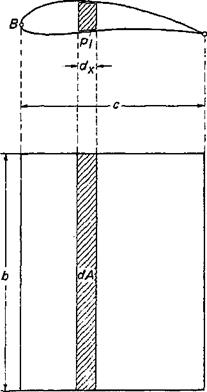Figure 2-5 Notations for the computation of lift from the pressure distribution on the airfoil.

Bernoulli equation. From Fig. 2-4, the velocities on the upper and lower surfaces of the airfoil are (wM+ilw) and (w„ — dw), respectively. The Bernoulli equation then furnishes for the pressure difference

‘Ap=-pt — pu = (u’oo + A w)2 —|- (?./;oo — A w)2 = 2o v’oo A w

where the assumption has been made that the magnitudes of the circulatory velocities on the lower and upper surfaces are equal, Awi — Awu = Aw.

By integration, the total lift of the airfoil is consequently obtained as

Jap dA=b f dp dx (А) І	(2-13 a)
C 2gbWoo / Aw dx	(2-13 b)
J в

The integration has been carried from the leading to the trailing edge (length of airfoil chord c).

The circulation along any line Taround the wing surface is

./’= Jwdl
(0

С В c

Г— fAwdx— f Aw dx — 2 f Aw dx (2-14 b)

B, u C, l В

The first integral in the first equation is to be taken along the upper surface, the second along the lower surface of the wing. From Eq. (2-13b) the lift is then given by

L = gbw00r (2-15)

This equation was found first by Kutta [35] in 1902 and independently by Joukowsky [31] in 1906 and is the exact relation, as can be shown, between lift and circulation. Furthermore, it can be shown that the lift acts normal to the direction of the incident flow.