Magnitude and Formation of Circulation

If the magnitude of the circulation is known, the Kutta-Joukowsky formula, Eq. (2-15), is of practical value for the calculation of lift. However, it must be clarified as to what way the circulation is related to the geometry of the wing profile, to the velocity of the incident flow, and to the angle of attack. This interrelation cannot be determined uniquely from theoretical considerations, so it is necessary to look for empirical results.

The technically most important wing profiles have, in general, a more or less sharp trailing edge. Then the magnitude of the circulation can be derived from experience, namely, that there is no flow around the trailing edge, but that the fluid flows off the trailing edge smoothly. This is the important Kutta flow-off condition, often just called the Kutta condition.

For a wing with angle of attack, yet without circulation (see Fig. 2-6a), the rear stagnation point, that is, the point at which the streamlines from the upper and lower sides recoalesce, would lie on the upper surface. Such a flow pattern would be possible only if there were flow around the trailing edge from the lower to the upper surface and, therefore, theoretically (in inviscid flow) an infinitely high velocity at the trailing edge with an infinitely high negative pressure. On the other hand, in the case of a very large circulation (see Fig. 2-6b) the rear stagnation point would be on the lower surface of the wing with flow around the trailing edge from above. Again velocity and negative pressure would be infinitely high.

Experience shows that neither case can be realized; rather, as shown in Fig.

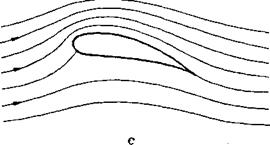
2- 6c, a circulation forms of the magnitude that is necessary to place the rear stagnation point exactly on the sharp trailing edge. Therefore, no flow around the trailing edge occurs, either from above or from below, and smooth flow-off is established. The condition of smooth flow-off allows unique determination of the magnitude of the circulation for bodies with a sharp trading edge from the body shape and the inclination of the body relative to the incident flow direction. This statement is valid for the inviscid potential flow. In flow with friction, a certain reduction of the circulation from the value determined for frictionless flow is observed as a result of viscosity effects.

For the formation of circulation around a wing, information is obtained from

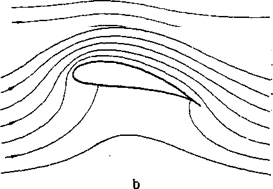Figure 2-6 Flow around an airfoil for various values of circulation, (a) Circulation Г= 0: rear stagnation point on upper surface. (b) Very large circulation: rear stagnation point on lower sur­face. (c) Circulation just sufficient to put rear stagnation point on trailing edge. Smooth flow – off: Kutta condition satisfied.

the conservation law of circulation in frictionless flow (Thomson theorem). This states that the circulation of a fluid-bound line is constant with time. This behavior will be demonstrated on a wing set in motion from rest, Fig. 2-7. Each fluid-bound line enclosing the wing at rest (Fig. 2-7a) has a circulation Г = 0 and retains, therefore, Г-0 at all later times. Immediately after the beginning of motion, frictionless flow without circulation is established on the wing (as shown in Fig.

2- 6a), which passes the sharp trailing edge from below (Fig. 2-lb). Now, because of friction, a left-turning vortex is formed with a certain circulation —Г. This vortex quickly drifts away from the wing and represents the so-called starting or initial vortex — Г (Fig. 2-lc).

For the originally observed fluid-bound line, the circulation remains zero, even though the line may become longer with the subsequent fluid motion. It continues, however, to encircle the wing and starting vortex. Since the total circulation of this fluid-bound line remains zero for all times according to the Thomson theorem, somewhere within this fluid-bound line a circulation must exist equal in magnitude to the circulation of the starting vortex but of reversed sign. This is the circulation +Г of the wing. The starting vortex remains at the starting location of the wing and is, therefore, some time after the beginning of the motion sufficiently far away from the wing to be of negligible influence on the further development of the flow field. The circulation established around the wing, which produces the lift, can be
replaced by one or several vortices within the wing of total circulation +Г as far as the influence on the ambient flow field is concerned. They are called the bound vortices.* From the above discussions it is seen that the viscosity of the fluid, after all, causes the formation of circulation and, therefore, the establishment of lift. In an inviscid fluid, the original flow without circulation and, therefore, with flow around the trailing edge, would continue indefinitely. No starting vortex would form and, consequently, there would be no circulation about the wing and no lift.

Viscosity of the fluid must therefore be taken into consideration temporarily to explain the evolution of lift, that is, the formation of the starting vortex. After establishment of the starting vortex and the circulation about the wing, the calculation of lift can be done from the laws of frictionless flow using the Kutta-Joukowsky equation and observing the Kutta condition.

*In three-dimensional wing theory (Chaps. 3 and 4) so-called free vortices are introduced. These vortices form the connection, required by the Helmholtz vortex theorem, between the bound vortices of finite length that stay with the wing and the starting vortex that drifts off with the flow. In the case of an airfoil of infinite span, which has been discussed so far, the free vortices are too far apart to play a role for the flow conditions at a cross section of a two-dimensional wing. Therefore only the bound vortices need to be considered.

Figure 2-7 Development of circulation during set­ting in motion of a wing, (a) Wing in stagnant fluid. (b) Wing shortly after beginning of motion; for the liquid line chosen in {a), the circulation Г — 0; because of flow around the trailing edge, a vortex forms at this station, (c) This vortex formed by flow around the trailing edge is the so-called starting vortex — Г; a circulation +Г develops consequently around the wing.