Coordinate Systems

Coordinates are ordered algebraic numbers called triples or n-tuples. Coordinate systems are abstract entities that establish the one-to-one corre­spondence between the elements of the Euclidean three-space and the coordinates.

Cartesian coordinate systems are coordinate systems in the Euclidean space for which the Cartesian metric As2 = JT &xf holds.

Coordinate axes are the geometrical images of mathematical scales of algebraic numbers.

Coordinate transformation is a relabeling of each element in Euclidean space with new coordinates according to a certain algorithm. A coordinate system is said to be associated with a frame if the coordinates of the frame points are time invariant. All coordinate systems embedded in one frame form a class X. All classes over all frames form the entity of the allowable coordinate systems.

These definitions necessitate some explanations. Coordinates are arranged as num­bered elements of matrices, e. g., the coordinates of the velocity vector v! B, ex­pressed in the Earth coordinate system }E, are

Kf =

The triple occupies three ordered positions in the column matrix. The moment of inertia tensor, expressed in the body coordinate system )B, exhibits the 9-tuple of ordered elements

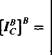in in iз /21 hi І23 hi hi hs_

By the way, not every matrix and its elements constitute the coordinates of a ten­sor. There must exist a one-to-one correspondence between the three-dimensional

Euclidean space and the coordinates. For instance, the three velocity coordinates are related to the three orthogonal directions of Euclidean space by

~Vl~		first direction
v2	О	second direction
Уз.		third direction

The moment of inertia tensor, on the other hand, has two directions associated with each element.

Because we are dealing with physical quantities, their numerical coordinates imply certain units of measure. The same units are embedded in every coordinate, e. g., v і, l’2, and t>3 all have the units of meters per second. This requirement to give measure to the coordinates leads to the geometrical concept of coordinate axes. They can be envisioned as rulers, etched with the unit measures, and given a positive direction.

At this point we pause and compare coordinate systems with frames of ref­erence. We defined a frame as a physical entity, consisting of points without relative movement. On the other hand, coordinate systems are mathematical ab­stracts without physical existence. This distinction is essential. Let me again quote Truesdell,3 “It is necessary to distinguish sharply between changes of frame and transformation of coordinate systems.” This separation will enable us to model the dynamics of flight vehicles in a coordinate-independent form, using points and frames, and defer the coordination and numerical evaluation until the building of the simulation.

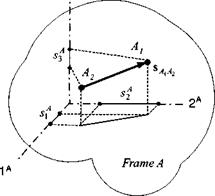
Let us explore this conversion process. Given frame A and two of its points A) and A2 (see Fig. 2.1), the displacement vector of point A1 wrt A2 is sAlAl. This vector is a well-defined quantity without reference to a coordinate system. Now we create a Cartesian coordinate system that establishes one-to-one relationships between the three-dimensional Euclidean space and the coordinates of the dis­placement vector. Designating it by ]A, we have one particular matrix realization

3A

of the displacement vector

The coordinates are shown in Fig. 2.1, superimposed on the coordinate axes. We label the axes in the 1 – 2 – 3 sequence with the name of the coordinate system as superscript. If the coordinates do not change in time, the coordinate system ]A is said to be associated with frame A. There are many, actually an infinite number of coordinate systems that have the same characteristic. They form a class K, the so-called associated coordinate systems with frame A.

Moreover, there are other coordinate systems. Picture a spear A, whose center – line is modeled by the displacement vector вд, д2, with point Ai marking the tip and A2 the tail. We already discussed the coordinating in the associated coordi­nate systems of its frame A. But suppose, you as observer, modeled by frame B, watch the spear in flight. In a coordinate system ]B associated with your frame, the centerline would have the coordinates

[*а, а2]В =

However, the coordinates are now changing in time. Your frame has a whole class К of such coordinate systems, just like the frame of the spear. There could be many frames (persons) present. All of these classes of coordinate systems form an entity, called the allowable coordinate systems.

Converting from one coordinate system to another is a relabeling process:

Because our coordinate systems are Cartesian, the relabeling algorithm is the multiplication of a 3 x 3 matrix with the coordinates of the vector

We symbolize the transformation matrix by [T]BA, meaning that it establishes the ]B coordinates wrt the]A coordinates. Notice my strict adherence to the double­index convention, reading from left to right, В —*■ A, and linking them with the words with respect to. Equation (2.1) is abbreviated by

[sa, a2]B = тВА[*д, д2]А (2.2)

The substance of the spear has not changed. We just have expressed the coordinates

of its centerline in two different coordinate systems. If the coordinate systems are associated with frames that change attitude relative to each other, the elements of T{t)BA are, as in our spear example, a function of time. Only if they are part of the same frame or other fixed frames are the elements constant.

By convention and convenience we use only right-handed Cartesian coordinate systems. (This terminology refers to the motion of the right hand, symbolically rotating the 1-axes into the 2-axis—shortest distance—while the index finger points in the positive direction of the З-axis.) We use them exclusively because they have the pleasant feature of their determinants always being positive one and their inverse equaling the transpose.

The discussion of Euclidean space would be incomplete without mentioning other coordinate systems that satisfy the Euclidean metric. Best known among them are the cylindrical and spherical coordinates. They are also orthogonal in the infinitesimal small sense of the Euclidean metric. However, only Cartesian coordi­nates satisfy the finite orthogonality of the Cartesian metric within the Euclidean space. With the definition of Cartesian coordinate systems in place, we can finally turn to the definition of tensors.