Geographic coordinate system

As you become comfortable with the Earth system, you want to navigate on the surface of the Earth. A grid, blanketing the Earth’s surface, determines any point you want to reach. It consists of lines of longitude and latitude. Longitude is divided into ±180° with the posi­tive direction starting at the Greenwich meridian in an easterly direction. Latitude is measured from the equator, positive to the north from 0 to 90° and negative south.

Inside of simulations it is better to work with radians. Longitude can extend from 0 to 2л or ±л and latitude between ±л/2. Yet, to be kind to the customer, you can allow the data to be input in degrees, minutes, and seconds, and in turn you convert your output to the same units. The unit of arc minutes takes on a particular significance on a great circle like the longitude meridians or the equator because the nautical mile is defined as the arc length of 1 min. Ergo, the circumference of the Earth on the equator is 60 x 360 = 21,600 n miles.

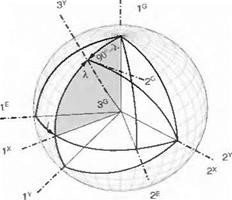
At a specific point on the surface of the Earth, with its longitude l and latitude X, the geographic coordinate system ]G is defined as follows: The 1° axis points north, the 3° axis points at the center of the Earth, and the 2° axis, pointing east, completes the right-handed coordinate system.

To relate the geographic coordinate system to the Earth system requires a few steps (refer to Fig. 3.15). The first transformation is from ]E to an intermediate system ]x with the longitude angle Z, symbolically written as ]x <—]£, followed by another intermediate system ]F, obtained through the compliment of the latitude angle 90° — X, or symbolically ]r —— ]x.

3E з* Fig. 3.15 Geographic wrt Earth coordinates.

Before we formulate the complete transformation, let us determine the TM of these two steps:

[T]YE = [7X90° – Я)]га[Г(/)]ж sink 0 —cos Я cos / sin / o" II 0 1 0 —sin/ cos / 0 cos Я 0 sink 0 0 1

sin Я cos/ sin Я sin/ —cos Я —sin / cos / 0

cos Я cos / cos Я sin / sin Я

Notice the first transformation [T]XE is about the 3£ axis, followed by the trans­formation [T]1** about the 2X axis.

To reach the geographic axes, we have to make a 180-deg somersault. The 1G and 3G axes take the opposite direction of the lr and 3K axes, respectively, while the 2g axis maintains the same sense as 2V. How do we determine this TM? We go back to Eq. (3.5) and visualize the base vectors associated with the preferred coordinate system ]G being expressed in the ]y system. From this perspective we obtain the somersault transformation

Шг		‘-І	0	0"
Шг	=	0	1	0
[£зГ		0	0	-1

Stringing all of the transformations together,

[:T]GE = [7180o)]Gy [7X90° – Я)]га[7Х/)]ж

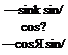yields the important TM of geographic wrt Earth coordinates:

As a vehicle moves across the Earth, its longitude and latitude coordinates change and so does the TM [TGE. This phenomenon has led to the expression, “the geographic coordinate system is attached to the vehicle and its origin moves with it,” a perspective that attributes physical substance to coordinate systems.

We are taking the “road less traveled” and follow an interpretation that is con­sistent with our premise that coordinate systems are purely mathematical entities. If you inspect Eq. (3.13), all you see are longitude and latitude angles. The TM, therefore, does not depend on an origin moving with the vehicle. We need only the longitude and latitude angles of the vehicle. As it moves over the Earth, the directions of the coordinate axes will change. However, the altitude of the vehi­cle is irrelevant. Therefore, you do not have to keep track of a coordinate origin travelling with the vehicle. Coordinate systems have no origins!

The Iе and 2° axes are tangential to the Earth at the longitude and latitude of the vehicle. At least that is true for our current assumption that a spherical Earth is adequate for our modeling tasks. Later, in Sec. 10.1.2, for sophisticated six-DoF simulations we will consider the Earth to be a spheroid. There we will introduce the geodetic coordinate ]D, which is tangential to the spheroid at the vehicle’s latitude and longitude. Its 3D axis does not point at the center of the Earth anymore. This direction will be maintained by the 3G axis as before, and for that reason the geographic system will be renamed in that section as the geocentric system.