Inertia Ellipsoid

The MOI tensor portrays a vivid geometrical interpretation, which is useful for the investigation of rigid-body dynamics. Being a real symmetric tensor, it has several important characteristics: it is positive definite, has three positive eigenval­ues, has three orthogonal eigenvectors, and can be diagonalized by an orthogonal coordinate transformation with the eigenvalues as diagonal elements.

As we have seen, the axial MOI about axis n through reference point R is according to Eq. (6.3) in body coordinates

/Я = [й]*[/!]Я[Л]*

= І\П + hin + /33П3 + 2/і2«іП2 + 2/23И2П3 + 2/31П3И1 (6.11)

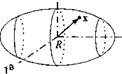
Interestingly, this scalar equation in quadratic form has a geometric representation. Because the eigenvalues of [/B]B are always real and positive, the geometrical surface, defined by Eq. (6.11), is an ellipsoid. If we introduce the normalized vector [х]в = пвIy/Tn, we obtain the equation for the MOI ellipsoid:

1=ИВ[7|]ВМВ

— hX + І22х2 + /33*3 + ^I2XX2 + 2/23X2X3 + 2Ij, iXt, X (6.12)

Referring to Fig. 6.5, x is the displacement vector of a surface element relative to the center point R. A large value of |jc| means that the axial MOI /„ about this vector is small and vice versa.

If the body axes are principal axes, then [IB]B is a diagonal matrix, and Eq. (6.12) simplifies to

1 — hx + І2Х2 T /3X3 (6.13)

where 11, /2, /3 are the principal MOIs. They determine the lengths of the three semi-axes of the MOI ellipsoid

The radius of gyration pn is that distance from the axis at which all mass is concentrated such that the axial MOI can be calculated from /„ = pynf. We use

it to get another expression for the surface vector:

Thus, the magnitude of the vector to a point on the inertia ellipsoid is inversely proportional to the radius of gyration about the direction of this vector. For example, in Fig. 6.5 the MOI about the third axis is greater than that about the second axis.

The directions of the eigenvectors e,e2, «з are the principal axes. If they are known in an arbitrary coordinate system [e]A, [e2]A, [ез]А, then the transforma­tion matrix

[ci]A

[T]DA = [e2]A

_ [c3]A.

transforms the MOI tensor into its diagonal form

[/diagonal]0 = [Г]°А[/]А[Ї]Ш

with the eigenvalues as principal MOIs.

Example 6.4 Shapes with Planar Symmetry

If a body with uniform mass distribution has a plane of symmetry, then one of its principal axes is normal to this plane. We validate this statement by the example of Fig. 6.6. The wing section has a plane of symmetry coinciding with the Is, 3® axes. According to Eq. (6.2), the products of inertia containing the components SiR2 are zero because their right and left components cancel. Thus

/и 0 I13

[/f]B= 0 h 0

/із 0 hi

and I2 is the principal MOI.

At no time did I assume the body to be rigid. Definitions and theorems of this section are valid for nonrigid as well as rigid bodies, and therefore, elastic structures are not excluded. However, a difficulty arises describing a frame for such an elastic body. Because, by definition, frame points are mutually fixed, we cannot use the particles of an elastic structure to make up the body frame. Instead, we have to idealize the structure and define the frame to coincide either with a no-load

situation, the initial shape, or some average condition. Yet, do not be discouraged! The definition of the MOI does not rely on a body frame, but rather a collection of particles, mutually fixed or moving, which we designate as B. Only in the future, when we use the body as reference frame of the rotational derivative, do we need to specify a true frame. In those situations we will limit the discussion to rigid bodies.

The MOI joins the rotation tensors in our arsenal of second-order tensors. Both have distinctly different characteristics. Whereas the MOI tensor models a physical property of mass, the rotation tensor relates abstract reference frames. Their traits are contrasted by symmetrical vs orthogonal properties. However, both share the invariant property of tensors under any allowable coordinate transformation; and in both cases points and frames are sufficient to define them. Now we have reached the time to make the MOI come alive by joining it with angular velocity to form the angular momentum.